题目内容
4.已知点O是△ABC的外接圆的圆心,AB=10,AC=6,则$\overrightarrow{AO}$•$\overrightarrow{BC}$的值是( )| A. | 64 | B. | 32 | C. | -32 | D. | -64 |
分析 根据$\overrightarrow{BC}$=$\overrightarrow{AC}$$-\overrightarrow{AB}$,把要求的式子化为 $\overrightarrow{AO}$•$\overrightarrow{BC}$=$\overrightarrow{AO}$$•\overrightarrow{AC}$$-\overrightarrow{AO}$$•\overrightarrow{AB}$,再根据向量数量积的几何意义即可得到答案.
解答 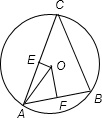 解:解:设AC的中点为E,AB的中点为 F,
解:解:设AC的中点为E,AB的中点为 F,
∵△ABC的外接圆圆心为O,AB=2,AC=3,
∴$\overrightarrow{BC}$=$\overrightarrow{AC}$$-\overrightarrow{AB}$,$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\overrightarrow{AO}$$•\overrightarrow{AC}$$-\overrightarrow{AO}$$•\overrightarrow{AB}$
=|AC|×|AE|-|AF|×|AB|=6×$\frac{6}{2}$-10×$\frac{10}{2}$
=-32,
故选:C
点评 本题考查了向量的平行四边形法则、三角形外接圆的性质、数量积运算定义,考查了推理能力与计算能力,属于中档题

练习册系列答案
相关题目
9.已知圆心C在直线2x+y=0上,且圆C夹在两条平行线l1:x+y+5=0与l2:x+y-3=0之间,圆上的点到两条平行线的最小距离均为$\sqrt{2}$,则圆C的标准方程为( )
| A. | (x-1)2+(y-2)2=2 | B. | (x-1)2+(y+2)2=4 | C. | (x-2)2+(y+4)2=2 | D. | (x-1)2+(y+2)2=2 |
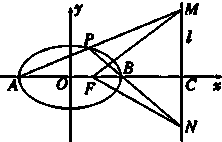 已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.
已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,F为椭圆的右焦点,且AF=3,离心率e=$\frac{1}{2}$,又P是椭圆上异于A、B的任意一点,直线AP、BP分别交直线l:x=m(m>2)于M、N两点,l交x轴于C点.