题目内容
6．已知椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上一点P到其右焦点的距离为8，则点P到椭圆左准线的距离为$\frac{5}{2}$．分析 求出椭圆的a，b，c，由第一定义，求得P到椭圆左焦点距离，再由离心率公式和椭圆的第二定义，即可求得所求值．
解答 解：椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的a=5，b=3，c=4．
则P到椭圆两个焦点距离之和为10，
P到椭圆右焦点距离为8，则P到椭圆左焦点距离为2，
由于离心率e=$\frac{c}{a}$=$\frac{4}{5}$，
又离心率为P到左焦点的距离与点P到椭圆左准线的距离的比，
即有点P到椭圆左准线的距离为：$\frac{2}{\frac{4}{5}}$=$\frac{5}{2}$．
故答案为：$\frac{5}{2}$．
点评 本题考查椭圆的第一定义和第二定义，考查离心率公式及运用，考查运算能力，属于中档题和易错题．
练习册系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
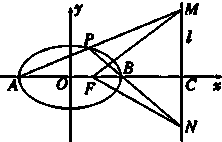已知A、B为椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，F为椭圆的右焦点，且AF=3，离心率e=$\frac{1}{2}$，又P是椭圆上异于A、B的任意一点，直线AP、BP分别交直线l：x=m（m＞2）于M、N两点，l交x轴于C点．