题目内容
正三棱锥的高为1,底面边长为2 ,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为
,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为

 ,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为
,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为 
9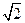 +6
+6 ;
; -2
-2
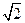 +6
+6 ;
; -2
-2过PA与球心O作截面PAE,与平面PCB交于PE,与平面ABC交于AE(如图)
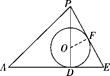
∵△ABC是正三角形,
∴AE即是△ABC中BC边上的高,又是BC边上的中线,
又因为正三棱锥的高PD=1通过球心,所以D是三角形△ABC的重心,
∵底面正三角形边长为2
 ,
,∴DE=
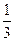 AE=
AE=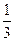 ×
×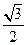 ×2
×2 =
=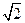 ,
,又PE为侧面之高,所以PE=
 =
= .
.高球的半径为r,由△POF∽△PED,知
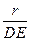 =
=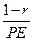 ,
,所以
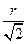 =
=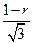 ,r=
,r= -2,
-2,所以
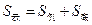
=3×
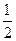 ×2
×2 ×
× +
+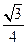 ×
×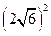
=9
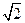 +6
+6 .
.
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 中,
中, ,
, ,直线
,直线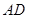 与底面
与底面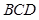 所成角为
所成角为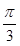 ,则此时三棱锥外接球的表面积为( )
,则此时三棱锥外接球的表面积为( )










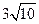
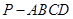 的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为
的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为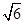 ,则这个球的表面积为_________.
,则这个球的表面积为_________. .
.