题目内容
四面体的六条棱中,有五条棱长都等于a.
(1)求该四面体的体积的最大值;
(2)当四面体的体积最大时,求其表面积.
(1)求该四面体的体积的最大值;
(2)当四面体的体积最大时,求其表面积.
(1) a3(2)
a3(2)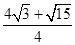 a2
a2
 a3(2)
a3(2)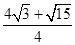 a2
a2(1)如图,在四面体ABCD中,设AB=BC=CD=AC=BD=a,AD=x,取AD的中点为P,BC的中点为E,连结BP、EP、CP.得到AD⊥平面BPC,
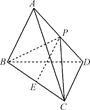
∴VA-BCD=VA-BPC+VD-BPC= ·S△BPC·AP+
·S△BPC·AP+ S△BPC·PD=
S△BPC·PD= ·S△BPC·AD=
·S△BPC·AD= ·
· ·a
·a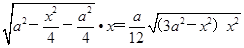 ≤
≤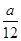 ·
· =
= a3(当且仅当x=
a3(当且仅当x= a时取等号).
a时取等号).
∴该四面体的体积的最大值为 a3.
a3.
(2)由(1)知,△ABC和△BCD都是边长为a的正三角形,△ABD和△ACD是全等的等腰三角形,其腰长为a,底边长为 a,
a,
∴S表=2× a2+2×
a2+2× ×
× a×
a×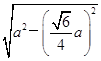 =
= a2+
a2+ a×
a× =
= a2+
a2+ =
=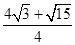 a2.
a2.

∴VA-BCD=VA-BPC+VD-BPC=
 ·S△BPC·AP+
·S△BPC·AP+ S△BPC·PD=
S△BPC·PD= ·S△BPC·AD=
·S△BPC·AD= ·
· ·a
·a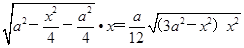 ≤
≤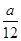 ·
· =
= a3(当且仅当x=
a3(当且仅当x= a时取等号).
a时取等号).∴该四面体的体积的最大值为
 a3.
a3.(2)由(1)知,△ABC和△BCD都是边长为a的正三角形,△ABD和△ACD是全等的等腰三角形,其腰长为a,底边长为
 a,
a,∴S表=2×
 a2+2×
a2+2× ×
× a×
a×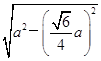 =
= a2+
a2+ a×
a× =
= a2+
a2+ =
=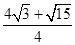 a2.
a2.
练习册系列答案
相关题目
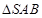 ,
, 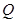 为底面圆周上一点.
为底面圆周上一点.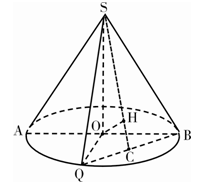
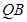 的中点为
的中点为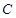 ,
,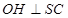 ,求证
,求证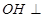 平面
平面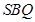 ;
;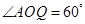 ,
,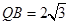 ,求此圆锥的全面积.
,求此圆锥的全面积.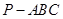 中,
中,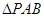 和
和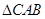 都是以
都是以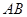 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,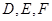 分别是
分别是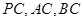 的中点.
的中点.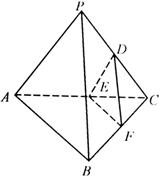
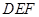 //平面
//平面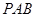 ;
;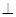
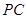 ;
;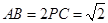 ,求三棱锥
,求三棱锥 ,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为
,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为 
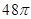 ,则此正方体边长为
,则此正方体边长为 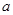 的三棱锥
的三棱锥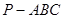 的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )
的侧面都是直角三角形,且四个顶点都在一个球面上,则球的表面积为( )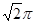

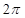
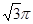
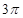
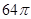


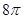
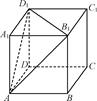
 ABCD的体积为
ABCD的体积为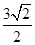 ,底面边长为
,底面边长为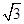 ,则以O为球心,OA为半径的球的表面积为 .
,则以O为球心,OA为半径的球的表面积为 .