题目内容
已知三棱锥 中,
中, ,
, ,直线
,直线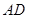 与底面
与底面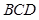 所成角为
所成角为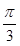 ,则此时三棱锥外接球的表面积为( )
,则此时三棱锥外接球的表面积为( )
 中,
中, ,
, ,直线
,直线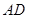 与底面
与底面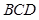 所成角为
所成角为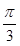 ,则此时三棱锥外接球的表面积为( )
,则此时三棱锥外接球的表面积为( )A. | B. | C. | D. |
B
试题分析:如下图所示,取
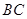 的中点
的中点 ,连接
,连接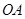 、
、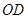 ,易证
,易证 ,所以
,所以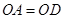 ,
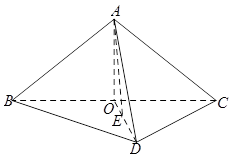
,
易证
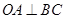 ,
,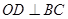 ,且
,且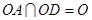 ,
,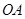 、
、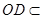 平面
平面 ,
,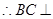 平面
平面 ,
,过点
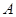 在平面
在平面 内作
内作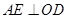 ,由于
,由于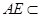 平面
平面 ,
,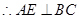 ,
,由于
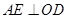 ,
,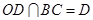 ,
,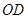 、
、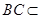 平面
平面 ,
,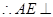 平面
平面
因此,
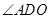 为直线
为直线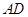 与平面
与平面 所成的角,所以
所成的角,所以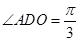 ,由于
,由于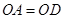 ,
,所以
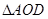 为等边三角形,
为等边三角形,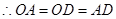 ,
,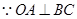 ,且
,且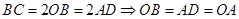 ,
,由勾股定理得
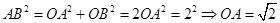 ,易知
,易知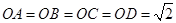 ,
,所以
 为三棱锥
为三棱锥 外接球的球心,其半径为
外接球的球心,其半径为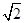 ,所以其外接球的表面积为
,所以其外接球的表面积为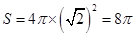 ,
,故选B.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 中,
中, ,
, ,
, .将
.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示. ⊥平面
⊥平面 ;(2)求几何体
;(2)求几何体 的体积.
的体积.
 中,平面
中,平面 平面
平面 ,
, 于点
于点 ,且
,且 ,
, ,
, 

 ,
, ,求三棱锥
,求三棱锥
 的边长为
的边长为 ,点
,点 分别在边
分别在边 上,
上,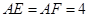 ,现将△
,现将△ 沿线段
沿线段 折起到△
折起到△ 位置,使得
位置,使得 .
.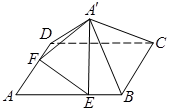
 的体积;
的体积; 的夹角.
的夹角. 的半圆面,则该圆锥的体积为 .
的半圆面,则该圆锥的体积为 .  的各顶点都在一半径为
的各顶点都在一半径为 的球面上,球心
的球面上,球心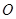 在
在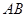 上,且有
上,且有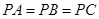 ,底面
,底面 中
中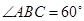 ,则球与三棱锥的体积之比是 .
,则球与三棱锥的体积之比是 .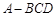 中,
中,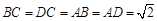 ,
,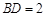 ,平面
,平面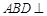 平面
平面 ,
,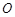 为
为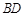 中点,点
中点,点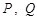 分别为线段
分别为线段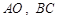 上的动点(不含端点),且
上的动点(不含端点),且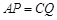 ,则三棱锥
,则三棱锥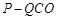 体积的最大值为________.
体积的最大值为________.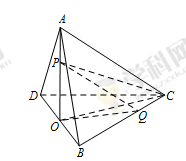
 ,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为
,内有一个球与四个面都相切(如图), 则棱锥的表面积和球的半径为 
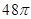 ,则此正方体边长为
,则此正方体边长为