题目内容
【题目】已知向量 ![]() =(sinx,2cosx),
=(sinx,2cosx), ![]() =(5
=(5 ![]() cosx,cosx),函数f(x)=
cosx,cosx),函数f(x)= ![]()
![]() +|
+| ![]() |2﹣
|2﹣ ![]() .
.
(1)求函数f(x)的最小正周期;
(2)若x∈( ![]() ,
, ![]() )时,f(x)=﹣3,求cos2x的值;
)时,f(x)=﹣3,求cos2x的值;
(3)若cosx≥ ![]() ,x∈(﹣
,x∈(﹣ ![]() ,
, ![]() ),且f(x)=m有且仅有一个实根,求实数m的取值范围.
),且f(x)=m有且仅有一个实根,求实数m的取值范围.
【答案】
(1)解:由函数f(x)= ![]()
![]() +|
+| ![]() |2﹣
|2﹣ ![]() .
.
可得:f(x)= ![]() sinxcosx+2cos2x+sin2x+4cos2x﹣
sinxcosx+2cos2x+sin2x+4cos2x﹣ ![]()
= ![]() sin2x+
sin2x+ ![]() ﹣
﹣ ![]() cos2x+3+3cos2x-
cos2x+3+3cos2x- ![]()
= ![]() sin2x+
sin2x+ ![]() cos2x
cos2x
=5sin(2x+ ![]() )
)
∴函数f(x)的最小正周期T= ![]()
(2)解:当x∈( ![]() ,
, ![]() )
)
可得2x+ ![]() ∈[
∈[ ![]() ,2π]
,2π]
∵f(x)=﹣3,即5sin(2x+ ![]() )=﹣3
)=﹣3
∴sin(2x+ ![]() )=-
)=- ![]()
∴cos(2x+ ![]() )=
)= ![]()
∴cos2x=cos[(2x+ ![]() )-
)- ![]() )=cos(2x+
)=cos(2x+ ![]() )cos
)cos ![]() )+sin(2x+
)+sin(2x+ ![]() )sin
)sin ![]() )=
)= ![]()
(3)解:由题意∵cosx≥ ![]() ,x∈(﹣
,x∈(﹣ ![]() ,
, ![]() ),
),
∴x∈[- ![]() ,
, ![]() ],
],
∵f(x)=m有且仅有一个实根,即函数f(x)与y=m的图象只有一个交点.
f(x)=5sin(2x+ ![]() )
)
∴2x+ ![]() ∈[-
∈[- ![]() ,
, ![]() ]
]
令2x+ ![]() =t,则t∈[-
=t,则t∈[- ![]() ,
, ![]() ],那么f(x)=5sin(2x+
],那么f(x)=5sin(2x+ ![]() )转化为g(t)=5sint与y=m的图象只有一个交点.
)转化为g(t)=5sint与y=m的图象只有一个交点.
,g(t)=5sint图象如下:
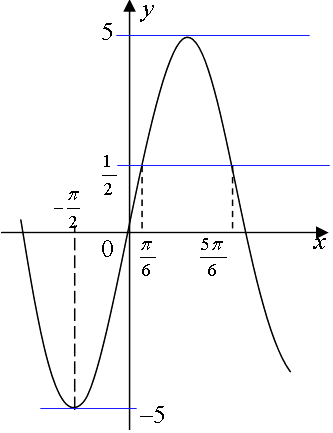
从图象可看出:当﹣5≤m ![]() 或m=5时,函数y=m与g(t)=5sint只有一个交点.故得实数m的取值范围是{m|﹣5≤m
或m=5时,函数y=m与g(t)=5sint只有一个交点.故得实数m的取值范围是{m|﹣5≤m ![]() 或m=5}
或m=5}
【解析】(1)根据平面向量数量积运算建立关系,求解f(x),利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期(2)根据x∈( ![]() ,
, ![]() )时,出内层函数的取值范围,f(x)=﹣3,化简f(x),可求cos2x的值.(3)根据cosx≥
)时,出内层函数的取值范围,f(x)=﹣3,化简f(x),可求cos2x的值.(3)根据cosx≥ ![]() ,x∈(﹣
,x∈(﹣ ![]() ,
, ![]() ),确定x的范围,利用数形结合法作f(x)=m有且仅有一个实根,可得答案.
),确定x的范围,利用数形结合法作f(x)=m有且仅有一个实根,可得答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

