题目内容
【题目】已知单调递增的等比数列![]() 满足:
满足: ![]() ,
, ![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() 成立的正整数
成立的正整数![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)(1)根据等比数列![]() 满足:
满足: ![]() ,
, ![]() 列出关于首项
列出关于首项![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,从而可得数列
的值,从而可得数列![]() 的通项公式;(2)先求数列
的通项公式;(2)先求数列![]() 的通项公式,利用错位相减法求得前
的通项公式,利用错位相减法求得前![]() 项和为
项和为![]() ,将
,将![]() 再代入
再代入![]() 整理,解不等式即可求出
整理,解不等式即可求出![]() 成立的正整数
成立的正整数![]() 的最小值.
的最小值.
试题解析:(1)设等比例列![]() 的首项为
的首项为![]() ,公比为q
,公比为q
依题意,有![]() ,解之得
,解之得![]() 或
或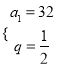 ,
,
又数列![]() 单调递增,
单调递增, ![]()
(2)依题意, ![]()
![]() ①
①
![]() ②
②
由①—②得: ![]()
![]()
![]() ,
, ![]() ,即
,即![]() ,
, ![]() 当
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
, ![]() 使
使![]() ,成立的正整数
,成立的正整数![]() 的最小值为
的最小值为![]() .
.
【 方法点睛】本题主要考查等比数列的通项公式与求和公式以及错位相减法求数列的的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列, ![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”与“
”与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目