题目内容
已知向量a="(cos" α,sin α),b="(cos" β,sin β),0<β<α<π.
(1)若|a-b|=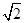 ,求证:a⊥b;
,求证:a⊥b;
(2)设c=(0,1),若a+b=c,求α,β的值.
(1)若|a-b|=
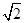 ,求证:a⊥b;
,求证:a⊥b;(2)设c=(0,1),若a+b=c,求α,β的值.
(1)见解析 (2) α= ,β=
,β=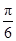
 ,β=
,β=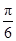
(1)证明:由|a-b|=
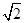 得
得(cosα-cos β)2+(sinα-sinβ)2=2,
即2-2cosαcosβ-2sinαsinβ=2,
∴cosαcosβ+sinαsinβ=0,
即a·b=0,
∴a⊥b.
(2)解:因为a+b=(cosα+cosβ,sin α+sinβ)=(0,1),
所以
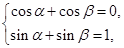
由此得,cosα=cos(π-β),
由0<β<π,得0<π-β<π.
又0<α<π,
故α=π-β.
代入sinα+sinβ=1,得sinα=sinβ=
 ,
,而α>β,
所以α=
 ,β=
,β=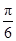 .
.
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
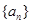 是公比为
是公比为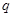 的无穷等比数列,下列
的无穷等比数列,下列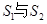 ;②
;②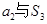 ;③
;③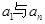 ;④
;④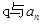 .
. 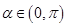 ,且
,且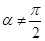 ,当
,当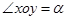 时定义平面坐标系
时定义平面坐标系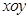 为
为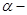 仿射坐标系,在
仿射坐标系,在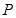 的斜坐标这样定义:
的斜坐标这样定义: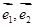 分别为与
分别为与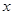 轴、
轴、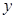 轴正向相同单位向量,若
轴正向相同单位向量,若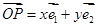 ,则记为
,则记为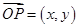 ,那么在以下的结论中,正确的有 .
,那么在以下的结论中,正确的有 .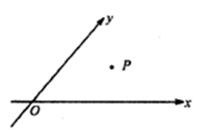
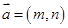 ,
,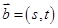 ,若
,若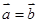 ,则
,则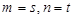 ;
;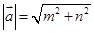 ;
;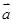
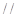
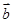 ,则
,则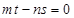 ;
;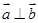 ,
,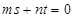 ;
;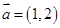 ,
,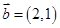 ,若
,若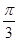 ,则
,则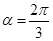 。
。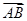 ="(cos" 18°,cos 72°),
="(cos" 18°,cos 72°), 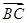 ="(2cos" 63°,2cos 27°),则△ABC面积为( )
="(2cos" 63°,2cos 27°),则△ABC面积为( )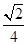

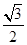
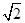
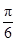 ,则
,则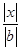 的最大值等于 .
的最大值等于 .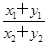 的值为( )
的值为( )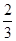
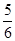
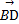 =2
=2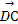 ,
,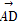 =m
=m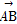 +n
+n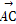 ,则
,则 的值为( )
的值为( )

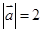 ,
,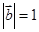 ,
,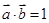 ,则向量
,则向量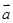 与
与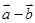 的夹角为 .
的夹角为 .