题目内容
已知平面上三个向量a、b、c的模均为1,它们相互之间的夹角均为120°.
(1)求证:(a-b)⊥c;
(2)若|ka+b+c|>1(k∈R),求k的取值范围.
(1)求证:(a-b)⊥c;
(2)若|ka+b+c|>1(k∈R),求k的取值范围.
(1)见解析(2)k>2或k<0
(1)证明:(a-b)·c=a·c-b·c
=|a||c|cos120°-|b||c|cos120°=0,∴(a-b)⊥c.
(2)解:|ka+b+c|>1?|ka+b+c|2>1?k2a2+b2+c2+2ka·b+2ka·c+2b·c>1.
∵|a|=|b|=|c|=1,且a、b、c夹角均为120°,
∴a2=b2=c2=1,a·b=b·c=a·c=-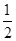 .
.
∴k2-2k>0,即k>2或k<0.
=|a||c|cos120°-|b||c|cos120°=0,∴(a-b)⊥c.
(2)解:|ka+b+c|>1?|ka+b+c|2>1?k2a2+b2+c2+2ka·b+2ka·c+2b·c>1.
∵|a|=|b|=|c|=1,且a、b、c夹角均为120°,
∴a2=b2=c2=1,a·b=b·c=a·c=-
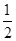 .
.∴k2-2k>0,即k>2或k<0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
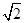 ,求证:a⊥b;
,求证:a⊥b; -1
-1 =
= +λ·
+λ· (λ∈R),试问:
(λ∈R),试问: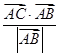 =1,
=1,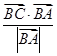 =2,则AB边的长度为( )
=2,则AB边的长度为( )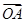 +
+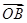 +
+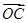 =0,则有( )
=0,则有( ) =2
=2
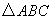 所在平面内的一点,且满足
所在平面内的一点,且满足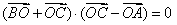 ,则
,则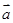 与
与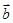 的夹角为
的夹角为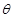 ,
,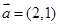 ,
,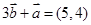 ,则
,则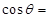 ________.
________.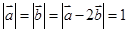 ,则
,则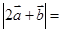 .
.