题目内容
4.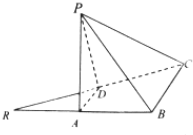 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC(Ⅰ)求证:BC⊥PB
(Ⅱ)求PC与平面ABCD所成角的余弦值.
分析 (Ⅰ)由已知条件AD∥BC,PA⊥AD,从而得到BC⊥PA,再由BC⊥AB,即可得到BC⊥平面PAB,从而得出BC⊥PB;
(Ⅱ)由PA⊥AD,PA⊥AB即可得到PA⊥平面ABCD,从而连接AC,∠PCA便是PC与平面ABCD所成角,从而求出AC,PC的长,在直角三角形PAC中即可求出cos∠PCA.
解答 解:(Ⅰ)证明:∵A、D分别是RB、RC的中点;
∴AD∥BC,∠PAD=∠RAD=∠RBC=90°;
∴PA⊥AD,PA⊥BC;
又BC⊥AB,PA∩AB=A;
∴BC⊥平面PAB;
∵PB?平面PAB;
∴BC⊥PB;
(Ⅱ)由PA⊥AD,PA⊥AB,AD∩AB=A;
∴PA⊥平面ABCD;
连接AC,则∠PCA是直线PC与平面ABCD所成的角;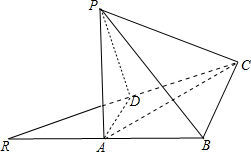 ∵AB=1,BC=2,∴AC=$\sqrt{5}$;
∵AB=1,BC=2,∴AC=$\sqrt{5}$;
又PA=1,PA⊥AC,∴PC=$\sqrt{6}$;
∴在Rt△PAC中,cos$∠PCA=\frac{AC}{PC}=\frac{\sqrt{5}}{\sqrt{6}}=\frac{\sqrt{30}}{6}$;
∴PC与平面ABCD所成角的余弦值为$\frac{\sqrt{30}}{6}$.
点评 考查三角形中位线的性质,弄清折叠前后不变的量,线面垂直的判定定理及其性质,线面角的概念及求法,直角三角形边的关系.

练习册系列答案
相关题目
13.为了得到函数y=$\frac{1}{2}$cos2x的图象,可以把函数y=$\frac{1}{2}$sin(2x+$\frac{π}{3}$)的图象上所有的点( )
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
14.已知函数f(x)=ex的图象与函数g(x)=|ln(-x)|的图象有两个交点A(x1,y1),B(x2,y2),则( )
| A. | $\frac{1}{10}$<x1x2<$\frac{1}{e}$ | B. | $\frac{1}{e}$<x1x2<1 | C. | 1<x1x2<e | D. | x1x2>e |