题目内容

9．已知等差数列{an}，Sn为数列{an}的前n项和，a3=7，S4=24．求等差数列通项公式an．

分析 由已知列方程组求得等差数列的首项和公差，代入等差数列的通项公式得答案．

解答 解：设等差数列{an}的首项为a1，公差为d，
由已知得$\left\{\begin{array}{l}{{a}_{1}+2d=7}\\{4{a}_{1}+6d=24}\end{array}\right.$，解得$\left\{\begin{array}{l}{{a}_{1}=3}\\{d=2}\end{array}\right.$．
∴an=3+2（n-1）=2n+1．

点评 本题考查等差数列的通项公式，是基础的计算题．

练习册系列答案
相关题目
16．执行如图所示的程序框图，若a=7．则输出的S=（　　）
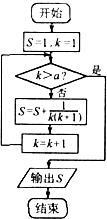
A．$\frac{6}{7}$B．$\frac{15}{8}$C．$\frac{13}{7}$D．$\frac{11}{6}$
17．设数列{an}的前n项和为Sn，且an+Sn=pn2+qn+r，其中p、q、r是常数，n∈N*．
（1）若数列{an}是等差数列且p=5，q=13，r=-2，求数列{an}的通项公式；
（2）①求证：当3p-q+r=0时，数列{an}为等差数列；
②若r=0，且{an}是首项为1的等差数列，设Tn=$\sqrt{1+\frac{1}{{{a}_{i}}^{2}}+\frac{1}{{{a}_{i+1}}^{2}}}$，Qn=$\sum_{i=1}^{n}$（Ti-1），试问：是否存在非零函数f（x），使得f（n）Q1Q2…Qn=1，对一切正整数n都成立，若存在，求出f（x）的解析式，否则，请说明理由．
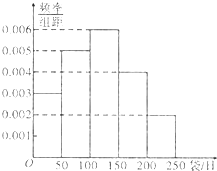17．如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图．将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．
（Ⅰ）估计日销售量的平均值；
（Ⅱ）求未来连续三天里，有两天日销售量不低于100袋且另一天销售量低于50袋的概率；
（Ⅲ）记X为未来三天里日销售量不低于150袋的天数，求X的分布列和均值（数学期望）．
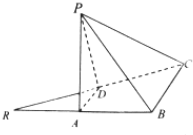4．如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2，点A，D分别是RB，RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连结PB，PC
（Ⅰ）求证：BC⊥PB
（Ⅱ）求PC与平面ABCD所成角的余弦值．
14．春运期间旅客增多，铁路局拟在深圳开往郑州的10辆列车基础上增加2辆临时列车，则不同的添加方法共有132种．
1．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的离心率等于2，它的焦点到渐近线的距离等于1，则该双曲线的方程为$\frac{{x}^{2}}{\frac{1}{3}}-{y}^{2}=1$．
18．已知（1+i）2=a+bi（a，b∈R，i为虚数单位），则a+b=2．
19．已知F1、F2分别为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点，A1、A2分别为其左、右顶点，过F2且与x轴垂直的直线l与椭圆相交于M、N两点．若四边形A1MA2N的面积等于2，且满足|$\overrightarrow{{A}_{1}{F}_{2}}$|=$\sqrt{2}$|$\overrightarrow{MN}$|+|$\overrightarrow{{A}_{2}{F}_{2}}$|．
（1）求此椭圆的方程；
（2）设⊙O的直径为F1F2，直线l：y=kx+m与⊙O相切，并与椭圆交于不同的两点P、Q，若$\overrightarrow{OP}$•$\overrightarrow{OQ}$=λ，且λ∈[$\frac{2}{3}$，$\frac{3}{4}$]，求△POQ的面积S的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网