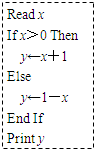题目内容
12.已知a>0,函数f(x)=$\frac{a}{x}$+|lnx-a|.(1)若对于任意x∈[1,e2],f(x)≤$\frac{3}{2}$恒成立,求实数a的取值范围;
(2)若a=1,求方程f[f(x)]=x解的个数.
分析 (1)由题意得$\frac{a}{x}$+|lnx-a|≤$\frac{3}{2}$,分a≥2与0<a<2讨论求函数的最值,从而化恒成立问题为最值问题即可;
(2)将函数写出分段形式,讨论x的范围和f(x)的范围,及函数的单调区间,结合零点存在定理,即可得到解的个数.
解答 解:(1)当由题意得,$\frac{a}{x}$+|lnx-a|≤$\frac{3}{2}$,
当a≥2时,上式可化为$\frac{a}{x}$-lnx+a≤$\frac{3}{2}$恒成立,
且为$\frac{a}{x}$-lnx+a在[1,e2]上是减函数,
故只需使a+a≤$\frac{3}{2}$,无解;
当0<a<2时,
f(x)=$\left\{\begin{array}{l}{\frac{a}{x}+lnx-a,x∈[{e}^{a},{e}^{2}]}\\{\frac{a}{x}-lnx+a,x∈[1.{e}^{a}]}\end{array}\right.$,
故f(x)在[1,ea]上是减函数,在[ea,e2]上是增函数,
故只需使$\left\{\begin{array}{l}{a+a≤\frac{3}{2}}\\{\frac{a}{{a}^{2}}+2-a≤\frac{3}{2}}\end{array}\right.$,解得$\frac{{e}^{2}}{2({e}^{2}-1)}$≤a≤$\frac{3}{2}$,
故实数a的取值范围是[$\frac{{e}^{2}}{2({e}^{2}-1)}$,$\frac{3}{2}$];
(2)当a=1时,f(x)=$\frac{1}{x}$+|lnx-1|,
当0<x<e时,f(x)=$\frac{1}{x}$-lnx+1,
则f′(x)=-$\frac{1}{{x}^{2}}$-$\frac{1}{x}$<0恒成立,
f(x)在(0,e)递减;
∴f(x)min=f(e)=$\frac{1}{e}$,
当x≥e时,f(x)=$\frac{1}{x}$+lnx-1,
则f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{1}{x}$=$\frac{x-1}{{x}^{2}}$>0恒成立,
f(x)在(e,+∞)递增.
∴f(x)min=f(e)=$\frac{1}{e}$,
当$\frac{1}{e}$≤f(x)≤e时,f(f(x))=$\frac{1}{f(x)}$+1-lnf(x),
当f(x)>e时,f(f(x))=$\frac{1}{f(x)}$+lnf(x)-1.
令f(x0)=e(0<x0<1),即有f(f(x0))=$\frac{1}{e}$,
可得f(f(x))在(0,x0)递减,(x0,e)递增,(e,+∞)递减.
由于f(f(x0))<x0,f(f(e))>e,
且y=x经过原点,由零点存在定理可得,
方程f[f(x)]=x在区间(0,x0),(x0,e),(e,+∞)上各有一解.
故共有3个解.
点评 本题考查了导数的综合应用及恒成立问题,同时考查函数方程的转化思想,以及零点存在定理的运用,属于中档题

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案| A. | [$\sqrt{5}$,5] | B. | [$\frac{3\sqrt{2}}{2}$,5] | C. | [$\frac{9}{2}$,25] | D. | [9,25] |
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{3-2\sqrt{2}}{3}$ |
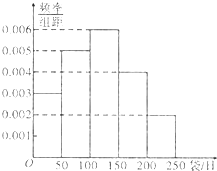 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.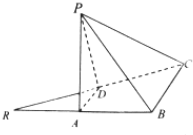 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC