题目内容
19.已知函数f(x)=2x3-3ax2+1,且x=1为函数f(x)的一个极值点.(1)求a的值;
(2)证明:f(x)≤2x2-3x2-x+ex.
分析 (1)由求导公式求出f′(x),根据题意和极值点的必要条件列出方程,求出a的值并进行验证;
(2)由(1)化简f(x)≤2x2-3x2-x+ex,再构造函数g(x)并求出导数,再求出函数的单调区间和最小值,即可证明结论成立.
解答 解:(1)由题意得,f′(x)=6x2-6ax,
∵x=1为函数f(x)的一个极值点,
∴f′(1)=6-6a=0,解得a=1,
经验证a=1符合条件,则a=1;
证明:(2)由(1)得,f(x)=2x3-3x2+1,
要证f(x)≤2x2-3x2-x+ex,
只需证ex-x-1≥0成立;
设g(x)=ex-x-1,则g′(x)=ex-1,
令g′(x)=ex-1=0,解得x=0,
∴当x∈(-∞,0)时,g′(x)<0;当x∈(0,+∞)时,g′(x)>0;
∴函数g(x)在(-∞,0)上递减,在(0,+∞)上递增;
则函数g(x)在x=1处取到极小值也是最小值,g(0)=0,
∴g(x)≥0成立,
故f(x)≤2x2-3x2-x+ex成立.
点评 本题考查了函数的导数与函数的单调性、极值、最值的关系,以及构造函数法证明不等式,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
9.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与抛物线y2=4x的焦点重合,则a+b的最大值为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | 2$\sqrt{2}$ |
 如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.
如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一定点,其坐为(x0,y0)(x0≠0),Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为$\frac{3}{2}$.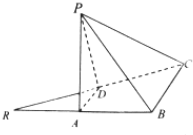 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC