题目内容
11.给出下列命题:①若$\overrightarrow a$•$\overrightarrow b$<0,则$\overrightarrow a$、$\overrightarrow b$的夹角为钝角;②若$\overrightarrow a$=(x1,y1),$\overrightarrow b$=(x2,y2),则$\overrightarrow a$∥$\overrightarrow b$?$\frac{x_1}{x_2}$=$\frac{y_1}{y_2}$;③若{${\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$}为空间的一组基底,则对于实数x、y、z满足x$\overrightarrow a$+y$\overrightarrow b$+z$\overrightarrow c$=$\overrightarrow 0$时,x2+y2+z2=0;④|$\overrightarrow p$+$\overrightarrow q$|•|$\overrightarrow p$-$\overrightarrow q$|=|${\overrightarrow p^2}$-${\overrightarrow q^2}$|;⑤$\overrightarrow p$在基底{$\overrightarrow i$,$\overrightarrow j$,$\overrightarrow k$}下的坐标为(1,2,3),则在基底{$\overrightarrow i$+$\overrightarrow j$,$\overrightarrow j$+$\overrightarrow k$,$\overrightarrow k$+$\overrightarrow i$}下的坐标为(0,2,1).其中正确的是③⑤(把你认为正确的命题序号都填上).
分析 举例说明①②错误;利用空间向量基本定理说明③正确;展开平面向量的数量积运算结合基本不等式说明④错误;利用坐标写出向量$\overrightarrow{p}$,进行等价转换后说明⑤正确.
解答 解:对于①,当$\overrightarrow a$、$\overrightarrow b$的夹角为π时,$\overrightarrow a•\overrightarrow b<0$,命题不正确;
对于②,当$\overrightarrow b=\overrightarrow 0$时命题不正确;
对于③,∵{${\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$}为空间的一组基底,∴${\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$为空间中三个非零且不共面的向量,
若实数x、y、z满足x$\overrightarrow a$+y$\overrightarrow b$+z$\overrightarrow c$=$\overrightarrow 0$,则x=y=0,即x2+y2+z2=0,命题正确;
对于④,$|{\overrightarrow p^2}-{\overrightarrow q^2}|=|{(\overrightarrow p+\overrightarrow q)•(\overrightarrow p-\overrightarrow q)}|$=$|\overrightarrow p+\overrightarrow q|•|\overrightarrow p-\overrightarrow q||cos<\overrightarrow p+\overrightarrow q,\overrightarrow p-\overrightarrow q>|$
≤$|\overrightarrow p+\overrightarrow q|•|\overrightarrow p-\overrightarrow q|$,当$\overrightarrow p+\overrightarrow q$与$\overrightarrow p-\overrightarrow q$同向共线时取等号,命题不正确;
对于⑤,$\overrightarrow p$在基底$\left\{{\overrightarrow i,\overrightarrow j,\overrightarrow k}\right\}$下的坐标为(1,2,3),即$\overrightarrow p=\overrightarrow i+2\overrightarrow j+3\overrightarrow k=0(\overrightarrow i+\overrightarrow j)+2(\overrightarrow j+\overrightarrow k)+1(\overrightarrow k+\overrightarrow i)$,命题正确.
∴正确的命题是③⑤.
故答案为:③⑤.
点评 本题考查命题的真假判断与应用,考查了平面向量的基本概念,是中档题.

| A. | [$\sqrt{5}$,5] | B. | [$\frac{3\sqrt{2}}{2}$,5] | C. | [$\frac{9}{2}$,25] | D. | [9,25] |
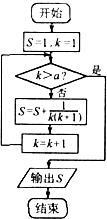
| A. | $\frac{6}{7}$ | B. | $\frac{15}{8}$ | C. | $\frac{13}{7}$ | D. | $\frac{11}{6}$ |
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{3-2\sqrt{2}}{3}$ |
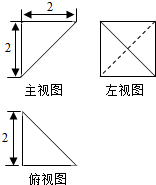
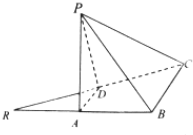 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC