题目内容

12．已知实数x，y满足logax+2logxa+logxy=4，其中常数a＞1，当y取最大值2时，对应的x的值为2．

分析 设logax=t，由已知化为logay=-（t-2）2+2≤2，可得2=a2，解得a，因此$2=lo{g}_{\sqrt{2}}x$，解得x即可．

解答 解：设logax=t，
∵logax+2logxa+logxy=4，其中常数a＞1，
∴logay=-（t-2）2+2≤2，当且仅当t=2时取等号．
∴y≤a2，
∴2=a2，解得a=$\sqrt{2}$，
∴$2=lo{g}_{\sqrt{2}}x$，解得x=2．
故答案为：2．

点评 本题考查了“换元法”、对数的换底公式、二次函数的单调性、考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
2．如图所示是一个几何体的三视图，则这个几何体外接球的表面积为12π．
3．已知动点A在椭圆 C：$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$（a＞b＞0）上，动点B在直线 x=-2上，且满足 $\overrightarrow{OA}⊥\overrightarrow{OB}$（O为坐标原点），椭圆C上点 $M（\frac{{\sqrt{3}}}{2}，3）$到两焦点距离之和为 4$\sqrt{3}$
（I）求椭圆C方程．
（Ⅱ）求|AB|取最小值时点A的坐标．
20．函数y=ax+1-3（a＞0，a≠1）过定点A，若点A在直线mx+ny=-2（m＞0，n＞0）上，则$\frac{1}{m}$+$\frac{1}{n}$的最小值为（　　）
A．3B．2$\sqrt{2}$C．$\frac{3+2\sqrt{2}}{2}$D．$\frac{3-2\sqrt{2}}{3}$
7．已知等差数列{an}的公差为d（d≠0），等比数列{bn}的公比为q（q＞0），且满足a1=b1=1，a2=b3，a6=b5．（1）求数列{an}的通项公式；
（2）证明：对一切n∈N*，令bn=an•an+1，都有$\frac{1}{4}$≤$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n}}$＜$\frac{1}{3}$．
17．设数列{an}的前n项和为Sn，且an+Sn=pn2+qn+r，其中p、q、r是常数，n∈N*．
（1）若数列{an}是等差数列且p=5，q=13，r=-2，求数列{an}的通项公式；
（2）①求证：当3p-q+r=0时，数列{an}为等差数列；
②若r=0，且{an}是首项为1的等差数列，设Tn=$\sqrt{1+\frac{1}{{{a}_{i}}^{2}}+\frac{1}{{{a}_{i+1}}^{2}}}$，Qn=$\sum_{i=1}^{n}$（Ti-1），试问：是否存在非零函数f（x），使得f（n）Q1Q2…Qn=1，对一切正整数n都成立，若存在，求出f（x）的解析式，否则，请说明理由．
7．设点A，B的坐标分别为（-a，0），（a，0），直线AC，BC相交于点C，且它们的斜率之积是-$\frac{{b}^{2}}{{a}^{2}}$（常数a，b为正实数）．
（Ⅰ）求点C的轨迹E的方程；
（Ⅱ）设O为坐标原点，P，Q为轨迹E上的动点，且OP⊥OQ，求$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$的值．
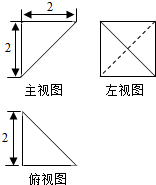
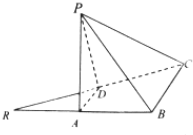4．如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2，点A，D分别是RB，RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连结PB，PC
（Ⅰ）求证：BC⊥PB
（Ⅱ）求PC与平面ABCD所成角的余弦值．
5．复数$\frac{2i}{1+i}$等于（　　）
A．1-iB．1+iC．-1+iD．-1-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网