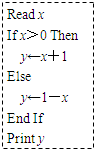题目内容
13.为了得到函数y=$\frac{1}{2}$cos2x的图象,可以把函数y=$\frac{1}{2}$sin(2x+$\frac{π}{3}$)的图象上所有的点( )| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
分析 由条件利用诱导公式、函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:把函数y=$\frac{1}{2}$sin(2x+$\frac{π}{3}$)的图象上所有的点向左平移$\frac{π}{12}$个单位,可得函数 y=$\frac{1}{2}$sin[2(x+$\frac{π}{12}$)+$\frac{π}{3}$]=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)=$\frac{1}{2}$cos2x的图象,
故选:C.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.函数y=ax+1-3(a>0,a≠1)过定点A,若点A在直线mx+ny=-2(m>0,n>0)上,则$\frac{1}{m}$+$\frac{1}{n}$的最小值为( )
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\frac{3+2\sqrt{2}}{2}$ | D. | $\frac{3-2\sqrt{2}}{3}$ |
5.复数$\frac{2i}{1+i}$等于( )
| A. | 1-i | B. | 1+i | C. | -1+i | D. | -1-i |
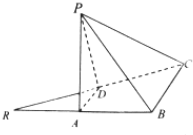 如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC
如图,已知等腰直角三角形RBC,其中∠RBC=90°,RB=BC=2,点A,D分别是RB,RC的中点,现将△RAD沿着边AD折起到△PAD位置,使PA⊥AB,连结PB,PC