题目内容
6.一个几何体的三视图如图所示,则这个几何体的表面积为2$\sqrt{3}$.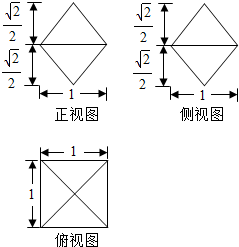
分析 根据几何体的三视图,得出该几何体是两个正四棱锥的组合体,根据图中数据求出它的表面积.
解答 解:根据几何体的三视图,得;
该几何体是上部为四棱锥,下部也为四棱锥的组合体,
且两个四棱锥是底面边长为1的正方形,高为$\frac{\sqrt{2}}{2}$正四棱锥;
所以该几何体的表面积为
S=8×$\frac{1}{2}$×1×$\sqrt{{{(\frac{1}{2})}^{2}+(\frac{\sqrt{2}}{2})}^{2}}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了利用空间几何体的三视图求表面积的应用问题,是基础题目.

练习册系列答案
相关题目
17.实系数一元二次方程x2+ax+2b=0的一个根在(0,1)上,另一个根在(1,2)上,则$\frac{b-3}{a-1}$的取值范围是( )
| A. | [1,3] | B. | (1,3) | C. | $[{\frac{1}{2},\frac{3}{2}}]$ | D. | $({\frac{1}{2},\frac{3}{2}})$ |
11.设函数y=3x与y=2-x的图象交点为(x0,y0),则x0所在的区间是( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
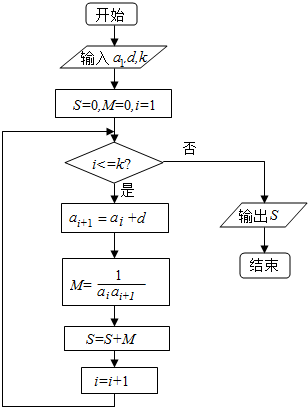 已知数列{an}的各项均为正数,观察程序框图
已知数列{an}的各项均为正数,观察程序框图