Question

1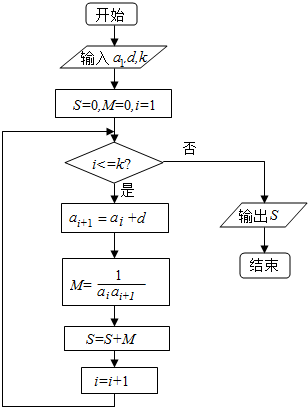．已知数列{a_n}的各项均为正数，观察程序框图
（1）若输入的a₁=1，d=1，k=3时，求输出的S的值
（2）写出k=4时，S的表达式（用a₁，a₂，a₃，a₄，a₅表示）
（3）若输入k=5，k=10时，分别有$S=\frac{5}{11}$和$S=\frac{10}{21}$．试求数列{a_n}的通项．

Answer 1

分析 模拟程序框图的运行过程，得出该程序运行后输出的S是什么，
然后对（1）中的数值进行计算，写出（2）k=4时S的表达式；
（3）中，由S的表达式，列出方程组求出a₁和d，即可求出a_n．

解答 解：（1）a₁=1，d=1，k=3时，
$S=\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}=1-\frac{1}{4}=\frac{3}{4}$；
（2）k=4时，$S=\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+\frac{1}{{{a_3}{a_4}}}+\frac{1}{{{a_4}{a_5}}}$；
（3）由程序框图知，S=$\frac{1}{a1a2}$+$\frac{1}{a2a3}$+…+$\frac{1}{akak+1}$，
∵数列{a_n} 是等差数列，设公差为d，
则有$\frac{1}{akak+1}$=$\frac{1}{d}$（$\frac{1}{ak}$-$\frac{1}{ak+1}$），
∴S=$\frac{1}{d}$（$\frac{1}{a1}$-$\frac{1}{a2}$+$\frac{1}{a2}$-$\frac{1}{a3}$+…+$\frac{1}{ak}$-$\frac{1}{ak+1}$）=$\frac{1}{d}$（$\frac{1}{a1}$-$\frac{1}{ak+1}$）；
k=5时，S=$\frac{5}{11}$；k=10时，S=$\frac{10}{21}$；
∴$\left\{\begin{array}{l}{\frac{1}{d}（\frac{1}{{a}_{1}}-\frac{1}{{a}_{6}}）=\frac{5}{11}}\\{\frac{1}{d}（\frac{1}{{a}_{1}}-\frac{1}{{a}_{11}}）=\frac{10}{21}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=-1}\\{d=-2}\end{array}\right.$（舍去）；
∴a_n=a₁+（n-1）d=2n-1．

点评 本题考查了程序框图的应用问题，也考查了数列求和的应用问题，考查了方程组的解法与应用问题，是综合题．