题目内容
11．设函数y=3x与y=2-x的图象交点为（x0，y0），则x0所在的区间是（ ）| A． | （0，$\frac{1}{2}$） | B． | （$\frac{1}{2}$，1） | C． | （1，2） | D． | （2，3） |
分析 作函数y=3x与y=2-x的图象，从而确定x0所在的区间是（0，1），再令x=$\frac{1}{2}$即可．
解答 解：作函数y=3x与y=2-x的图象如下，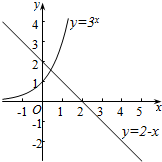
，
由图象可知，
函数y=3x与y=2-x的图象的交点在（0，1）之间；
故x0所在的区间是（0，1）；
又∵y=${3}^{\frac{1}{2}}$=$\sqrt{3}$，y=2-$\frac{1}{2}$=$\frac{3}{2}$，
∴$\sqrt{3}$＞$\frac{3}{2}$；
故x0所在的区间是（0，$\frac{1}{2}$）；
故选A．
点评 本题考查了数形结合的思想应用及恒成立问题．
练习册系列答案
全优点练单元计划系列答案
相关题目
19．随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额），如下表：
（1）求y关于x的回归方程 $\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（2）用所求的回归方程预测该地区2015年的人民币储蓄存款．
注：$\left\{\begin{array}{l}b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\\ a=\overline y-b\overline x\end{array}\right.$．
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
（2）用所求的回归方程预测该地区2015年的人民币储蓄存款．
注：$\left\{\begin{array}{l}b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}\\ a=\overline y-b\overline x\end{array}\right.$．
已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+2x（x＞0）}\\{0（x=0）}\\{{x}^{2}+mx（x＜0）}\end{array}\right.$为奇函数．
1．已知全集U={1，2，3，4，5，6}，集合A={1，3，5，6}，则∁UA等于（ ）
| A． | {1，3，5} | B． | {2，4，6} | C． | {2，4} | D． | {1，3，5，6} |