Question

16．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}-3，x≤0}\\{3x-2，x＞0}\end{array}\right.$，若|f（x）|＞ax，在x∈[-1，1]上恒成立，则实数a的取值范围（-2，0）．

Answer 1

分析 由题意画出函数y=|f（x）|及y=ax的图象，数形结合可得答案．

解答 解：作出函数y=|f（x）|及y=ax的图象如图，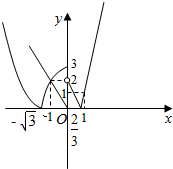

由图可知，当x∈[-1，1]时，要使|f（x）|＞ax恒成立，则
-2＜a＜0．
故答案为：（-2，0）．

点评 本题考查函数恒成立问题，考查了数形结合的解题思想方法，作图使得问题更加直观，是中档题．