题目内容
已知函数f(x)=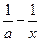 (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是增函数;
(2)若f(x)≤2x在(0,+∞)上恒成立,求a的取值范围;
(3)若f(x)在[m,n]上的值域是[m,n](m≠n),求a的取值范围.
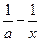 (a>0,x>0).
(a>0,x>0).(1)求证:f(x)在(0,+∞)上是增函数;
(2)若f(x)≤2x在(0,+∞)上恒成立,求a的取值范围;
(3)若f(x)在[m,n]上的值域是[m,n](m≠n),求a的取值范围.
(1)证明略 (2) a的取值范围是[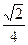 ,+∞)(3)0<a<
,+∞)(3)0<a<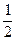
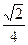 ,+∞)(3)0<a<
,+∞)(3)0<a<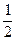
任取x1>x2>0,
f(x1)–f(x2)=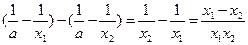
∵x1>x2>0,∴x1x2>0,x1–x2>0,
∴f(x1)–f(x2)>0,即f(x1)>f(x2),故f(x)在(0,+∞)上是增函数.
(2)解:∵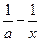 ≤2x在(0,+∞)上恒成立,且a>0,
≤2x在(0,+∞)上恒成立,且a>0,
∴a≥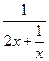 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
令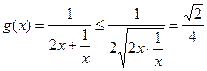
(当且仅当2x=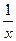 即x=
即x=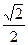 时取等号),
时取等号),
要使a≥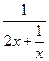 在(0,+∞)上恒成立,则a≥
在(0,+∞)上恒成立,则a≥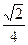 .
.
故a的取值范围是[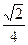 ,+∞).
,+∞).
(3)解: 由(1)f(x)在定义域上是增函数.
∴m=f(m),n=f(n),即m2–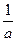 m+1=0,n2–
m+1=0,n2–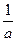 n+1=0
n+1=0
故方程x2–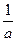 x+1=0有两个不相等的正根m,n,注意到m·n=1,
x+1=0有两个不相等的正根m,n,注意到m·n=1,
故只需要Δ=(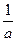 )2–4>0,由于a>0,则0<a<
)2–4>0,由于a>0,则0<a<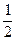 .
.
f(x1)–f(x2)=
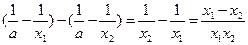
∵x1>x2>0,∴x1x2>0,x1–x2>0,
∴f(x1)–f(x2)>0,即f(x1)>f(x2),故f(x)在(0,+∞)上是增函数.
(2)解:∵
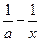 ≤2x在(0,+∞)上恒成立,且a>0,
≤2x在(0,+∞)上恒成立,且a>0,∴a≥
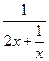 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,令
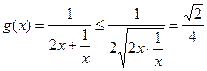
(当且仅当2x=
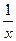 即x=
即x=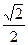 时取等号),
时取等号),要使a≥
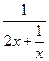 在(0,+∞)上恒成立,则a≥
在(0,+∞)上恒成立,则a≥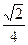 .
.故a的取值范围是[
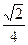 ,+∞).
,+∞).(3)解: 由(1)f(x)在定义域上是增函数.
∴m=f(m),n=f(n),即m2–
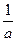 m+1=0,n2–
m+1=0,n2–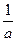 n+1=0
n+1=0故方程x2–
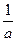 x+1=0有两个不相等的正根m,n,注意到m·n=1,
x+1=0有两个不相等的正根m,n,注意到m·n=1,故只需要Δ=(
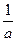 )2–4>0,由于a>0,则0<a<
)2–4>0,由于a>0,则0<a<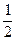 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
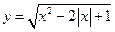 的曲线.
的曲线.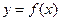 的反函数为
的反函数为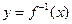 ,定义:若对给定的实数
,定义:若对给定的实数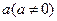 ,函数
,函数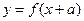 与
与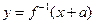 互为反函数,则称
互为反函数,则称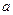 和性质”.
和性质”.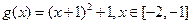 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由; 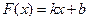 ,其中
,其中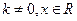 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得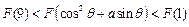 对任意的
对任意的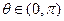 恒成立?若存在,求出
恒成立?若存在,求出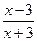
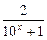 -1(x∈R)的反函数,函数g(x)的图像
-1(x∈R)的反函数,函数g(x)的图像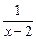 的图像关于y轴对称,设F(x)=f(x)+g(x).
的图像关于y轴对称,设F(x)=f(x)+g(x). 
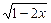 的值域是( )
的值域是( )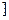
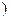
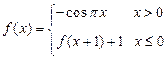 ,则
,则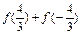 的值等于
的值等于 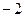
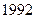 年底世界人口达到
年底世界人口达到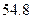 亿,若人口的年平均增长率为
亿,若人口的年平均增长率为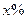 ,
,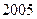 年底世界人口
年底世界人口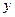 亿,那么
亿,那么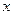 的函数关系式为 .
的函数关系式为 .