题目内容
已知函数f(x)=logm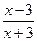
(1)若f(x)的定义域为［α，β］，（β＞α＞0），判断f(x)在定义域上的增减性，并加以说明；
(2)当0＜m＜1时，使f(x)的值域为［logm［m(β–1)］，logm［m(α–1)］］的定义域区间为［α,β］(β＞α＞0)是否存在？请说明理由.
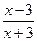
(1)若f(x)的定义域为［α，β］，（β＞α＞0），判断f(x)在定义域上的增减性，并加以说明；
(2)当0＜m＜1时，使f(x)的值域为［logm［m(β–1)］，logm［m(α–1)］］的定义域区间为［α,β］(β＞α＞0)是否存在？请说明理由.
（1）
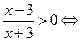x＜–3或x＞3.
∵f(x)定义域为［α,β］,∴α＞3
设β≥x1＞x2≥α，有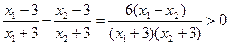
当0＜m＜1时，f(x)为减函数，当m＞1时，f(x)为增函数.
（2）若f(x)在［α,β］上的值域为［logmm(β–1),logmm(α–1)］
∵0＜m＜1, f(x)为减函数
∴
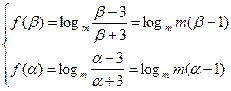
即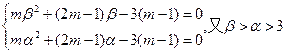
即α,β为方程mx2+(2m–1)x–3(m–1)=0的大于3的两个根
∴
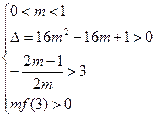∴0＜m＜
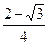
故当0＜m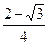＜时，满足题意条件的m存在.
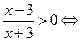x＜–3或x＞3.∵f(x)定义域为［α,β］,∴α＞3
设β≥x1＞x2≥α，有
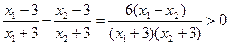
当0＜m＜1时，f(x)为减函数，当m＞1时，f(x)为增函数.
（2）若f(x)在［α,β］上的值域为［logmm(β–1),logmm(α–1)］
∵0＜m＜1, f(x)为减函数
∴
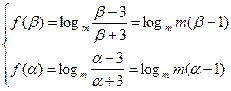
即
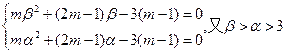
即α,β为方程mx2+(2m–1)x–3(m–1)=0的大于3的两个根
∴
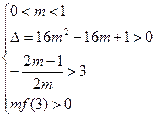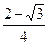
∴0＜m＜故当0＜m＜
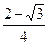时，满足题意条件的m存在.
练习册系列答案
相关题目
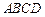中，已知
，
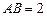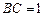，在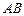
.
.
.
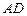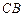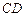上，分别截取
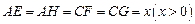，设四边形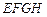
的面积为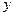
.
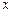之间的函数关系式；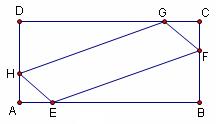
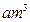时，只付基本费8元和每户的定额损耗费c元；若用水量超过
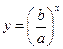的图象如图所示，求二次函数
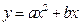的顶点的横坐标的取值范围．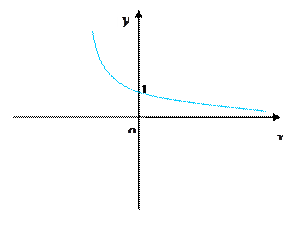
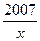)=3x，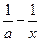
(a＞0,x＞0).
，
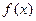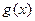分别由下表给出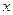
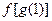的值为 当
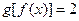时，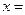
．