题目内容
9．深圳某商场为使销售空调和冰箱获得的总利润达到最大，对即将出售的空调和冰箱相关数据进行调查，得出下表：| 资金 | 每台空调或冰箱所需资金（百元） | 月资金供应数量 （百元） | |
| 空调 | 冰箱 | ||
| 成本 | 30 | 20 | 300 |
| 工人工资 | 5 | 10 | 110 |
| 每台利润 | 6 | 8 | |
分析 先设空调和冰箱的月供应量分别为x，y台，月总利润为z百元，依题意得列出约束条件和目标函数，最后依据线性规则的方法求出目标函数的最大值即可．
解答 解：设空调和冰箱的月供应量分别为x、y台，月总利润为z百元，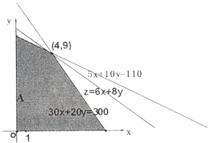
则$\left\{\begin{array}{l}{30x+20y≤300}\\{5x+10y≤110}\\{z=6x+8y}\end{array}\right.$，
作出可行域如图，作直线y=-$\frac{3}{4}$x的平行线，
当直线l过可行域上的一个顶A（4，9）即x、y分别为4、9时，z取得最大值，
∴空调和冰箱的月供应量分别为4台和9台时，月总利润为最大，
最大值为6•4+10•9=114（百元）．
点评 本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，注意解题方法的积累，属于中档题．
练习册系列答案
一课一练课时达标系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
4．函数y=x3-3x+1的单调减区间为（ ）
| A． | （1，2） | B． | （-1，1） | C． | （-2，-1） | D． | （-2，1） |
14．已知实数a，b，则“2a＞2b”是“log2a＞log2b”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
已知函数f（x）=Asin（ωx+ϕ）（A＞0，?＞0，|ϕ|＜$\frac{π}{2}$）的部分图象如图所示，则函数f（x）的解析式为y=2sin（πx+$\frac{π}{6}$）．