题目内容
17.已知等比数列{an}中,a2=$\frac{1}{3}$,公比q=$\frac{1}{3}$.(1)Sn为{an}的前n项和,证明:sn=$\frac{{3-{a_n}}}{2}$
(2)设bn=log3a1+log3a2+…+log3an,求数列bn的通项公式.
分析 (1)通过${a_2}=\frac{1}{3}$、q=$\frac{1}{3}$可知首项,进而可得通项、前n项和的表达式,整理即得结论;
(2)通过an=$\frac{1}{{3}^{n-1}}$、对数的性质可知log3an=-n+1,进而计算即得结论.
解答 (1)证明:∵${a_2}=\frac{1}{3}$,q=$\frac{1}{3}$
∴a1=$\frac{{a}_{2}}{q}$=$\frac{\frac{1}{3}}{\frac{1}{3}}$=1,
∴an=$\frac{1}{{3}^{n-1}}$,Sn=$\frac{3}{2}$(1-$\frac{1}{{3}^{n}}$),
∴Sn=$\frac{{3-{a_n}}}{2}$;
(2)解:∵an=$\frac{1}{{3}^{n-1}}$,
∴log3an=log3$\frac{1}{{3}^{n-1}}$=-n+1,
∴bn=log3a1+log3a2+…+log3an
=-(1+2+3+…+n)+n
=-$\frac{n(n+1)}{2}$+n
=-$\frac{n(n-1)}{2}$.
点评 本题考查数列的通项及前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
8.若复数z(1-i)=2+i(i是虚数单位),则$|{\overline z}|$=( )
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{3}{2}$ |
5.某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
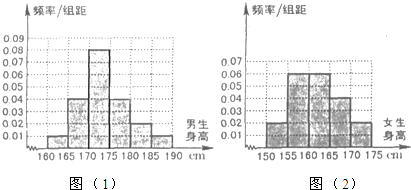
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:

(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
9.深圳某商场为使销售空调和冰箱获得的总利润达到最大,对即将出售的空调和冰箱相关数据进行调查,得出下表:
问:该商场怎样确定空调或冰箱的月供应量,才能使总利润最大?最大利润是多少?
| 资金 | 每台空调或冰箱所需资金(百元) | 月资金供应数量 (百元) | |
| 空调 | 冰箱 | ||
| 成本 | 30 | 20 | 300 |
| 工人工资 | 5 | 10 | 110 |
| 每台利润 | 6 | 8 | |