题目内容
【题目】已知函数f(x)=ex(2x﹣1),g(x)=ax﹣a(a∈R).
(1)若y=g(x)为曲线y=f(x)的一条切线,求a的值;
(2)已知a<1,若存在唯一的整数x0 , 使得f(x0)<g(x0),求a的取值范围.
【答案】
(1)解:f′(x)=ex(2x﹣1)+2ex=ex(2x+1),
设切点为(m,n),由题意可得a=em(2m+1),
又n=am﹣a=em(2m﹣1),
解方程可得,a=1或4 ![]()
(2)解:函数f(x)=ex(2x﹣1),g(x)=ax﹣a
由题意知存在唯一的整数x0使得f(x0)在直线y=ax﹣a的下方,
∵f′(x)=ex(2x﹣1)+2ex=ex(2x+1),
∴当x<﹣ ![]() 时,f′(x)<0,
时,f′(x)<0,
当x>﹣ ![]() 时,f′(x)>0,
时,f′(x)>0,
∴当x=﹣ ![]() 时,f(x)取最小值﹣2
时,f(x)取最小值﹣2 ![]() ,
,
当x=0时,f(0)=﹣1,当x=1时,f(1)=e>0,
直线y=ax﹣a恒过定点(1,0)且斜率为a,
故﹣a>f(0)=﹣1且f(﹣1)=﹣3e﹣1≥﹣a﹣a,
解得 ![]() ≤a<1.
≤a<1.
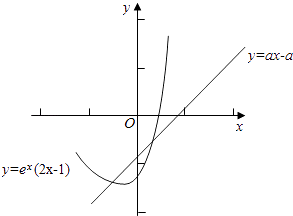
【解析】(1)求出导数,设出切点(m,n),求得切线的斜率,由切线的方程,可得a=em(2m+1),又n=am﹣a=em(2m﹣1),解方程可得a的值;(2)函数f(x)=ex(2x﹣1),g(x)=kx﹣k,问题转化为存在唯一的整数x0使得f(x0)在直线y=kx﹣k的下方,求导数可得函数的极值,数形结合可得﹣k>f(0)=﹣1且f(﹣1)=﹣3e﹣1≥﹣k﹣k,解关于k的不等式组可得.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目