题目内容
【题目】从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示. (Ⅰ)计算第三组的样本数;并估计该校高一年级1000名学生中身高在170厘米以下的人数;
(Ⅱ)估计被随机抽取的这100名学生身高的中位数、平均数.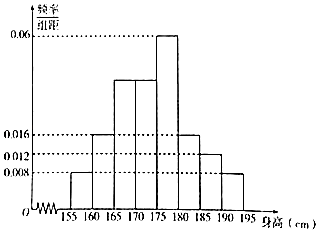
【答案】解: (Ⅰ)由第三组的频率为:[1﹣5×(0.008+0.008+0.012+0.016+0.016+0.06)]÷2=0.2,
则其样本数为:0.2×100=20,
由5×(0.008+0.016)+0.2=0.32,
则该校高一年级1000名学生中身高在170厘米以下的人数约为:0.32×1000=320(人)
(Ⅱ)前四组的频率为:5×(0.008+0.016)+0.4=0.52,0.52﹣0.5=0.02,
则中位数在第四组中,由 ![]() =0.1,可得:175﹣0.1×5=174.5,
=0.1,可得:175﹣0.1×5=174.5,
所以中位数为174.5 cm,
计算可得各组频数分别为:4,8,20,20,30,8,6,4,
平均数约为:(157.5×4+162.5×8+167.5×20+172.5×20+177.5×30+182.5×8+187.5×6+192.5×4)÷100=174.1(cm)
【解析】(Ⅰ)由频率分布直方图分析可得各数据段的频率,再由频率与频数的关系,可得频数.(Ⅱ)先求前四组的频率,进而可求中位数,计算可得各组频数,即可求解平均数.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案