题目内容
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴交于点D,且有|FA|=|FD|,当点A的横坐标为3时,△ADF为正三角形
(1)求C的方程
(2)延长AF交抛物线于点E,过点E作抛物线的切线l1 , 求证:l1∥l.
【答案】
(1)解:抛物线的焦点F( ![]() ,0),设D(t,0),则FD的中点为(
,0),设D(t,0),则FD的中点为( ![]() ,0).
,0).
∵|FA|=|FD|,∴3+ ![]() =|t﹣
=|t﹣ ![]() |,解得t=3+p或t=﹣3(舍).
|,解得t=3+p或t=﹣3(舍).
∵ ![]() =3,∴
=3,∴ ![]() ,解得p=2.
,解得p=2.
∴抛物线方程为y2=4x
(2)解:由(1)知F(1,0),设A( ![]() ,m)(m≠0),D(xD,0),
,m)(m≠0),D(xD,0),
∵|FA|=|FD|,则|xD﹣1|= ![]() +1,由xD>0得xD=
+1,由xD>0得xD= ![]() +2,即D(
+2,即D( ![]() +2,0).
+2,0).
∴直线l的斜率为kAD=﹣ ![]() .
.
设l1:y=kx+n(k≠0)与抛物线相切,代入可得ky2﹣4y+4n=0,△=0,所以E( ![]() ,
, ![]() ),
),
∵A,F,E三点共线,∴m( ![]() ﹣1)=
﹣1)= 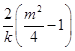 ,
,
解得k= ![]() 或k=﹣
或k=﹣ ![]() .
.
k= ![]() ,E与A重合,舍去,
,E与A重合,舍去,
∴k=﹣ ![]() ,
,
∴l1∥l.
【解析】(1)根据等边三角形的性质可知A点横坐标为FD的中点横坐标,列出方程解出p.(2)根据|FA|=|FD|列出方程得出A,D横坐标的关系,从而得出l的斜率,设l1方程,与抛物线方程联立,由判别式△=0得出l的截距与A点坐标的关系,求出E点坐标,利用A,F,E三点共线,即可证明结论.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目