题目内容
【题目】已知f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ;g(x)=1﹣x+
;g(x)=1﹣x+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣…﹣
﹣…﹣ ![]() ;设函数F(x)=[f(x+3)]2015[g(x﹣4)]2016 , 且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
;设函数F(x)=[f(x+3)]2015[g(x﹣4)]2016 , 且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
A.8
B.9
C.10
D.11
【答案】C
【解析】解:∵f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ,∴f′(x)=(1﹣x)+(x2﹣x3)+…+x2014
,∴f′(x)=(1﹣x)+(x2﹣x3)+…+x2014
=(1﹣x)(1+x2+x4+…+x2012)+x2014
当x=﹣1时,f′(x)=2×1007+1=2015>0,
当x≠﹣1时,f′(x)=(1﹣x)(1+x2+x4+…+x2012)+x2014
=(1﹣x) 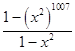 +x2014
+x2014
= ![]() >0,
>0,
∴f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() 在R上单调递增,
在R上单调递增,
∴f(0)=1>0,f(﹣1)=1﹣1﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣…﹣
﹣…﹣ ![]() <0,
<0,
∴函数f(x)在(﹣1,0)内有唯一零点,
由﹣1<x+3<0得:﹣4<x<﹣3,
∴f(x+3)在(﹣4,﹣3)上有唯一零点.
∴[f(x+3)]2015在(﹣4,﹣3)上有唯一零点,
∵g(x)=1﹣x+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣…﹣
﹣…﹣ ![]() ,
,
∴g′(x)=(﹣1+x)+(﹣x2+x3)+…﹣x2015
=﹣[(1﹣x)+(x2﹣x3)+…+x2015]
=﹣f′(x)<0,
∴g(x)在R上单调递减,
又g(1)=1﹣1 ![]() >0,
>0,
g(2)= ![]() <0,
<0,
当n≥2时, ![]() =
= ![]() <0,
<0,
∴g(2)<0.
∴g(x)在(1,2)上有唯一零点,
由1<x﹣4<2得:5<x<6,
∴g(x﹣4)在(5,6)上有唯一零点.
∴[g(x﹣4)]2016在(5,6)上有唯一零点.
∵F(x)=[f(x+3)]2015[g(x﹣4)]2016 ,
∴F(x)的零即为[f(x+3)]2015和[g(x﹣4)]2016的零点.
∴F(x)的零点区间为(﹣4,﹣3)∪(5,6).
又b,a∈Z,
∴(b﹣a)min=6﹣(﹣4)=10.
故选:C.

