题目内容
(本小题满分10分)已知函数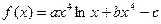
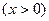 在
在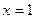 处取得极值
处取得极值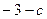 ,其中
,其中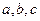 为常数.
为常数.
(1)求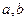 的值;
的值;
(2)讨论函数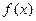 的单调区间;
的单调区间;
(3)若对任意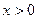 ,不等式
,不等式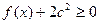 恒成立,求
恒成立,求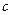 的取值范围.
的取值范围.
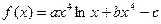
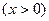 在
在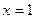 处取得极值
处取得极值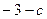 ,其中
,其中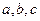 为常数.
为常数.(1)求
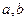 的值;
的值; (2)讨论函数
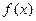 的单调区间;
的单调区间;(3)若对任意
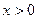 ,不等式
,不等式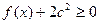 恒成立,求
恒成立,求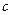 的取值范围.
的取值范围.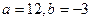 ,
,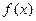 单调递减区间为
单调递减区间为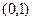 ,单调递增区间为
,单调递增区间为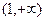
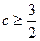 或
或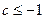
1)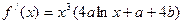 ,
,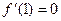 ,
,
∴
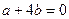 ,又
,又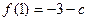 ,
,
∴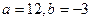 ; ………………5分
; ………………5分
(2)
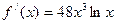 (
(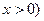
∴由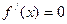 得
得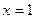 ,
,
当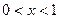 时,
时,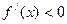 ,
,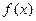 单调递减;
单调递减;
当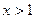 时,
时,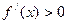 ,
,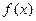 单调递增;
单调递增;
∴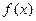 单调递减区间为
单调递减区间为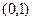 ,单调递增区间为
,单调递增区间为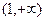 ……9分
……9分
(3)由(2)可知,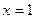 时,
时,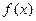 取极小值也是最小值
取极小值也是最小值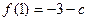 ,
,
依题意,只需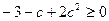 ,解得
,解得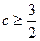 或
或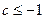 ………………10分
………………10分
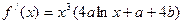 ,
,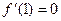 ,
,∴

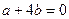 ,又
,又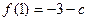 ,
, ∴
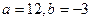 ; ………………5分
; ………………5分(2)

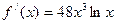 (
(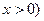
∴由
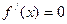 得
得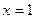 ,
,当
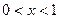 时,
时,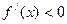 ,
,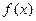 单调递减;
单调递减; 当
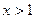 时,
时,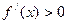 ,
,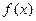 单调递增;
单调递增;∴
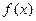 单调递减区间为
单调递减区间为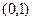 ,单调递增区间为
,单调递增区间为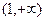 ……9分
……9分(3)由(2)可知,
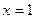 时,
时,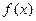 取极小值也是最小值
取极小值也是最小值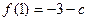 ,
,依题意,只需
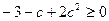 ,解得
,解得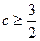 或
或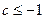 ………………10分
………………10分 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
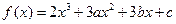 在
在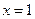 及
及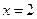 时取得极值.
时取得极值.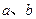 的值;
的值;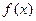 在
在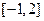 上的最大值是9,求
上的最大值是9,求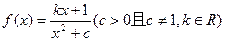 恰有一个极大值点和一个极小值点,其中的一个极值点是
恰有一个极大值点和一个极小值点,其中的一个极值点是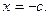
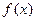 的另一个极值点;
的另一个极值点;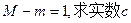 的值.
的值.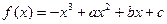 图象上的点
图象上的点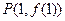 处的切线方程为
处的切线方程为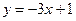 。若函数
。若函数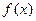 在
在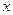 =-2处有极值,求
=-2处有极值,求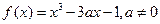 .
.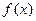 的单调区间;
的单调区间; 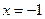 处取得极值,直线
处取得极值,直线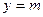 与
与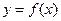 的图象有三个不同的交点,求
的图象有三个不同的交点,求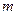 的取值范围。
的取值范围。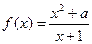 在
在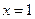 处取极值,则
处取极值,则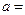
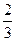 与
与 x=1时都取得极值.
x=1时都取得极值. 。
。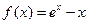 ,其中
,其中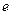 为自然对数的底数.
为自然对数的底数.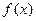 的最小值;
的最小值;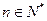 ,且
,且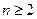 ,证明:
,证明: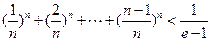 .
.