题目内容
已知函数f(x)=(2cos2x-1)sin 2x+ cos 4x.
cos 4x.
(1)求f(x)的最小正周期及最大值;
(2)若α∈ ,且f(α)=
,且f(α)= ,求α的值.
,求α的值.
 cos 4x.
cos 4x.(1)求f(x)的最小正周期及最大值;
(2)若α∈
 ,且f(α)=
,且f(α)= ,求α的值.
,求α的值.(1)最小正周期T=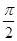 ,最大值为
,最大值为 .(2)α=
.(2)α=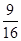 π
π
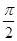 ,最大值为
,最大值为 .(2)α=
.(2)α=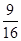 π
π(1)f(x)=(2cos2x-1)sin 2x+ cos 4x
cos 4x
=cos 2x·sin 2x+ cos 4x
cos 4x
= (sin 4x+cos 4x)=
(sin 4x+cos 4x)= sin
sin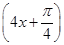 ,
,
∴f(x)的最小正周期T=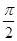 ,最大值为
,最大值为 .
.
(2)由f(α)= ,得sin
,得sin =1.
=1.
∵α∈ ,则
,则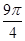 <4α+
<4α+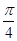 <
<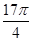 ,
,
所以4α+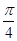 =
=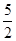 π,故α=
π,故α=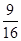 π.
π.
 cos 4x
cos 4x=cos 2x·sin 2x+
 cos 4x
cos 4x=
 (sin 4x+cos 4x)=
(sin 4x+cos 4x)= sin
sin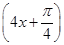 ,
,∴f(x)的最小正周期T=
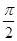 ,最大值为
,最大值为 .
.(2)由f(α)=
 ,得sin
,得sin =1.
=1.∵α∈
 ,则
,则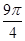 <4α+
<4α+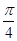 <
<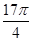 ,
,所以4α+
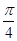 =
=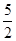 π,故α=
π,故α=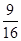 π.
π.
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 对称,则函数的解析式为________________.
对称,则函数的解析式为________________.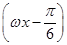 +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为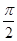 .
.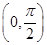 ,f
,f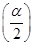 =2,求α的值.
=2,求α的值. .
. 的单调增区间;
的单调增区间; ,
, 求b+c的值.
求b+c的值.



 )(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈
)(ω>0)和g(x)=3cos(2x+φ)的图象的对称中心完全相同,若x∈ ,则f(x)的取值范围是______.
,则f(x)的取值范围是______.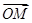 ·
·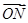 =0,则函数f(x)的最小正周期是________.
=0,则函数f(x)的最小正周期是________.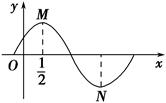
 在区间
在区间 上的最小值为 ( ).
上的最小值为 ( ).
 sin2x的最小正周期T为________.
sin2x的最小正周期T为________.