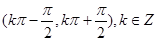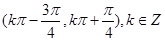题目内容
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( )


A.- | B.- | C. | D.- |
D
【思路点拨】由△EFG的高可得振幅A.由FG的长可得周期,从而得ω.由f(x)为奇函数可求φ,从而可求f(1).
解:由△EFG是边长为2的等边三角形,得高为 ,即A=
,即A= .
.
又FG为半个周期长故T=4,
∴ω=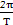 =
= .
.
又∵f(x)为奇函数,
∴φ=kπ+ ,k∈Z,
,k∈Z,
又∵0<φ<π,∴φ= .
.
∴f(x)= cos(
cos( x+
x+ ),
),
∴f(1)= cosπ=-
cosπ=- .
.
解:由△EFG是边长为2的等边三角形,得高为
 ,即A=
,即A= .
.又FG为半个周期长故T=4,
∴ω=
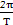 =
= .
.又∵f(x)为奇函数,
∴φ=kπ+
 ,k∈Z,
,k∈Z,又∵0<φ<π,∴φ=
 .
.∴f(x)=
 cos(
cos( x+
x+ ),
),∴f(1)=
 cosπ=-
cosπ=- .
.
练习册系列答案
相关题目
 ).
).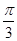 ,则f
,则f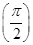 =________.
=________. ]上有零点,则实数m的取值范围为( )
]上有零点,则实数m的取值范围为( )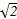 ]
] )的一个单调区间是 ( )
)的一个单调区间是 ( ) ]
] ,
, ]
] ]
] ),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )

 cos 4x.
cos 4x. ,且f(α)=
,且f(α)= ,求α的值.
,求α的值. 的值域为( )
的值域为( ) ,
,
 单调增区间为( )
单调增区间为( )