题目内容
已知函数f(x)=ex+2x2—3x
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2) 当x ≥1时,若关于x的不等式f(x)≥ax恒成立,求实数a的取值范围;
(3)求证函数f(x)在区间[0,1)上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,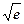 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2) 当x ≥1时,若关于x的不等式f(x)≥ax恒成立,求实数a的取值范围;
(3)求证函数f(x)在区间[0,1)上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,
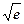 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。(1)(e+1)x-y-2=0
(2)a≤e-1
(3)x≈0.45
(2)a≤e-1
(3)x≈0.45
(1)f'(x)=ex+4x-3,则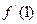 =e+1,
=e+1,
又f(1)=e—1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为
y-e+1=(e+1)(x-1),即:(e+1)x-y-2=0
(2)由f(x)≥ax,得ax≤ex+2 x2-3x,
∵x≥1 ,∴a≤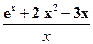
令g(x)=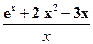 ,则g’(x)=
,则g’(x)=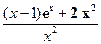
∵x≥1 ,∴g’(x)>0,∴g(x)在[1,+∞)上是增函数,
∴g(x)min=g(1)=e-1,
∴a的取值范围是a≤e-1,
(3)∵f'(0)=e0-3=-2<0,f'(1)=e+1>0, ∴f'(0)·f'(1)<0
令h(x)=f'(x)=ex+4x-3,
则h'(x)=ex+4>0,f'(x)在正[0,1]上单调递增,
∴.f'(x)在[0,1]上存在唯一零点,f(x)在[0,1]上存在唯一的极值点.
取区间[0,1]作为起始区间,用二分法逐次计算可知区间[0.3,0.6]的长度为0.3,所以该区间的中点x2=0.45,到区间端点的距离小于0.2,因此可作为误差不超过0.2一个极值点的相应x的值
∴函数y=f(x)取得极值时,相应x≈0.45.
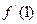 =e+1,
=e+1,又f(1)=e—1,
∴曲线y=f(x)在点(1,f(1))处的切线方程为
y-e+1=(e+1)(x-1),即:(e+1)x-y-2=0
(2)由f(x)≥ax,得ax≤ex+2 x2-3x,
∵x≥1 ,∴a≤
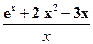
令g(x)=
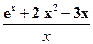 ,则g’(x)=
,则g’(x)=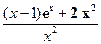
∵x≥1 ,∴g’(x)>0,∴g(x)在[1,+∞)上是增函数,
∴g(x)min=g(1)=e-1,
∴a的取值范围是a≤e-1,
(3)∵f'(0)=e0-3=-2<0,f'(1)=e+1>0, ∴f'(0)·f'(1)<0
令h(x)=f'(x)=ex+4x-3,
则h'(x)=ex+4>0,f'(x)在正[0,1]上单调递增,
∴.f'(x)在[0,1]上存在唯一零点,f(x)在[0,1]上存在唯一的极值点.
取区间[0,1]作为起始区间,用二分法逐次计算可知区间[0.3,0.6]的长度为0.3,所以该区间的中点x2=0.45,到区间端点的距离小于0.2,因此可作为误差不超过0.2一个极值点的相应x的值
∴函数y=f(x)取得极值时,相应x≈0.45.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 .
. 时,求函数
时,求函数 的极值;
的极值; ,有
,有 成立,求实数
成立,求实数 的取值范围.
的取值范围. .
. ,其中
,其中 ,则
,则 零点的个数是 ( )
零点的个数是 ( ) 在
在 上的最小值是 .
上的最小值是 . ,且
,且 .
. 的值;
的值; 的单调区间;
的单调区间; ,若函数
,若函数 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围. ,2]上恰有两解,求实数m的取值范围.
,2]上恰有两解,求实数m的取值范围. 是减函数的区间为 ( )
是减函数的区间为 ( )


