题目内容
已知函数 ,
,
(1)求 的单调递减区间;
的单调递减区间;
(2)若 在区间
在区间 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值.
 ,
,(1)求
 的单调递减区间;
的单调递减区间;(2)若
 在区间
在区间 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值.(1)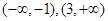 ;(2)
;(2)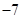 .
.
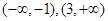 ;(2)
;(2)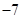 .
.试题分析:(1)对函数求导,可得
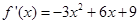 ,由
,由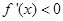 得函数的单调递减区间; (2)由函数的单调区间可知
得函数的单调递减区间; (2)由函数的单调区间可知 在
在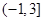 上单调递增.那么
上单调递增.那么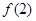 和
和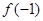 分别是
分别是 在区间
在区间 上的最大值和最小值,由最大值
上的最大值和最小值,由最大值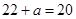 ,得
,得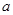 ,代回可求得最小值
,代回可求得最小值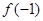 .
.解:(1)
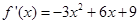 ,令
,令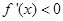 , ..2分
, ..2分解得
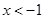 或
或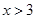 , .4分
, .4分所以函数
 的单调递减区间为
的单调递减区间为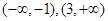 . .6分
. .6分(2)因为
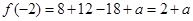 ,
,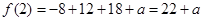 ,
,所以
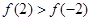 .∵
.∵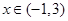 时,
时,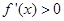 ,∴
,∴ 在
在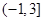 上单调递增.
上单调递增.又
 在
在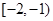 上单调递减,
上单调递减,所以
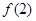 和
和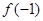 分别是
分别是 在区间
在区间 上的最大值和最小值. ..10分
上的最大值和最小值. ..10分于是有
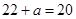 ,解得
,解得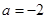 .故
.故 ,
,所以
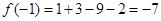 ,即函数
,即函数 在区间
在区间 上的最小值为
上的最小值为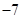 12分
12分
练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 .
. 时,求函数
时,求函数 的极值;
的极值;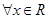 ,有
,有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 若当0
若当0 时,
时, 恒成立,则实数m的取值范围是 ( )
恒成立,则实数m的取值范围是 ( )
 内不是增函数的是( )
内不是增函数的是( )



 .
. 的方程f(x)=a在区间
的方程f(x)=a在区间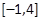 上有两个根,求a的取值范围.
上有两个根,求a的取值范围. 在
在 上单调递增,则实数
上单调递增,则实数 的取值范围是 .
的取值范围是 . ,其中
,其中 ,则
,则 零点的个数是 ( )
零点的个数是 ( )