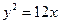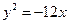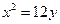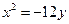题目内容
(本小题满分12分)设A、B分别是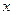 轴,
轴,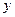 轴上的动点,P在直线AB上,且
轴上的动点,P在直线AB上,且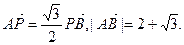
(1)求点P的轨迹E的方程;
(2)已知E上定点K(-2,0)及动点M、N满足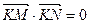 ,试证:直线MN必过
,试证:直线MN必过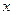 轴上的定点。
轴上的定点。
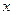 轴,
轴,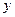 轴上的动点,P在直线AB上,且
轴上的动点,P在直线AB上,且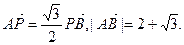
(1)求点P的轨迹E的方程;
(2)已知E上定点K(-2,0)及动点M、N满足
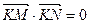 ,试证:直线MN必过
,试证:直线MN必过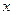 轴上的定点。
轴上的定点。(1)
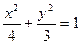
(2)直线MN必过
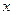 轴上的定点,证明略。
轴上的定点,证明略。(1)设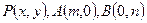 ,则
,则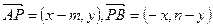
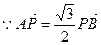 ,
,
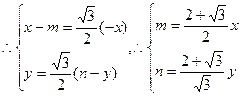
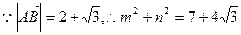
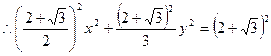 ,所以点P的轨迹方程为
,所以点P的轨迹方程为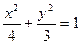 。
。
(2)设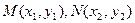 ,
,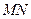 所在直线方程为
所在直线方程为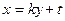 ,
,
联立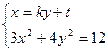 得
得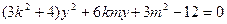 因为直线与椭圆有两个交点,所以
因为直线与椭圆有两个交点,所以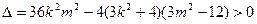 即
即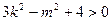 且
且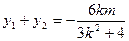
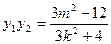 因为
因为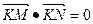 ,
,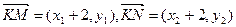 所以
所以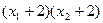
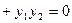 所以
所以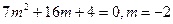 或
或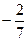
当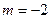 时,MN直线过点K与题意不符;当
时,MN直线过点K与题意不符;当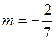 时,MN方程为
时,MN方程为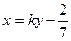 所以恒过定点(
所以恒过定点(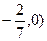 ,
,
即直线MN必过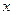 轴上的定点。
轴上的定点。
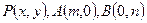 ,则
,则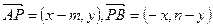
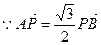 ,
,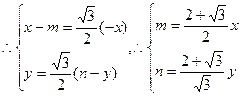
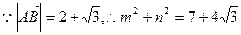
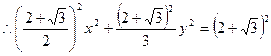 ,所以点P的轨迹方程为
,所以点P的轨迹方程为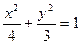 。
。(2)设
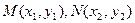 ,
,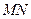 所在直线方程为
所在直线方程为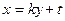 ,
,联立
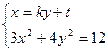 得
得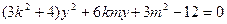 因为直线与椭圆有两个交点,所以
因为直线与椭圆有两个交点,所以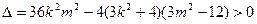 即
即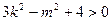 且
且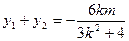
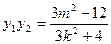 因为
因为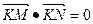 ,
,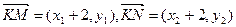 所以
所以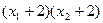
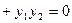 所以
所以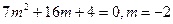 或
或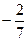
当
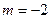 时,MN直线过点K与题意不符;当
时,MN直线过点K与题意不符;当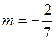 时,MN方程为
时,MN方程为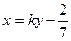 所以恒过定点(
所以恒过定点(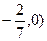 ,
,即直线MN必过
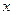 轴上的定点。
轴上的定点。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
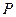 (4,
(4,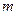 )到焦点的距离为5.
)到焦点的距离为5.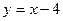 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证:
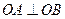 .
.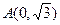 、
、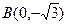 的距离之和为4.
的距离之和为4.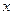 轴的垂线段PD,D为垂足,当P在曲线C上运动时,线段PD的中点M的轨迹是什么?
轴的垂线段PD,D为垂足,当P在曲线C上运动时,线段PD的中点M的轨迹是什么?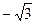 ,0),B是圆C:(x-
,0),B是圆C:(x-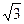 )2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.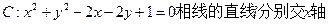 、y轴于
、y轴于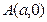 、
、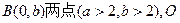 为原点。
为原点。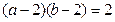 ;
;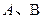 是圆
是圆 上满足条件
上满足条件 的两个点,其中O是坐标原点,分别过A、B作
的两个点,其中O是坐标原点,分别过A、B作 轴的垂线段,交椭圆
轴的垂线段,交椭圆 于
于 点,动点P满足
点,动点P满足 .(1)求动点P的轨迹方程;(2)设
.(1)求动点P的轨迹方程;(2)设 和
和 分别表示
分别表示 和
和 的面积,当点P在
的面积,当点P在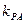 和
和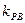 ,且满足
,且满足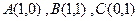 ,映射
,映射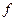 将
将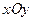 平面上的点
平面上的点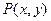 对应到另一个平面直角坐标系
对应到另一个平面直角坐标系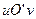 上的点
上的点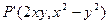 ,则当点
,则当点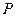 沿着折线
沿着折线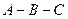 运动时,在映射
运动时,在映射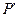 的轨迹是
的轨迹是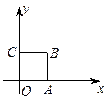
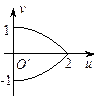
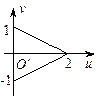
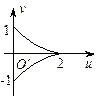
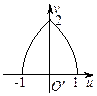
 相切的动圆圆心轨迹方程是( )
相切的动圆圆心轨迹方程是( )