题目内容
(本小题满分12分)
已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点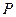 (4,
(4,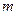 )到焦点的距离为5.
)到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线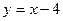 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证:
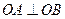 .
.
已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点
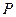 (4,
(4,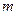 )到焦点的距离为5.
)到焦点的距离为5.(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线
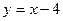 相交于不同的两点A、B,求证:
相交于不同的两点A、B,求证:
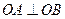 .
.解:(Ⅰ)由题意设抛物线方程为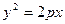
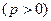 ,其准线方程为
,其准线方程为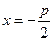 ,…2分
,…2分
∵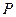 (4,
(4,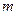 )到焦点的距离等于A到其准线的距离,
)到焦点的距离等于A到其准线的距离,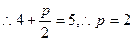
∴抛物线C的方程为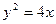 .
.  ………………………4分
………………………4分
(Ⅱ)由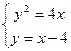 ,消去
,消去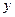 ,得
,得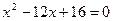 (*) ……………………6分
(*) ……………………6分
∵直线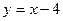 与抛物线相交于不同两点A、B,设
与抛物线相交于不同两点A、B,设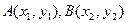 ,则有
,则有
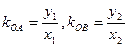
 ,则
,则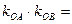
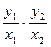 ………………………8分
………………………8分
因为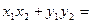
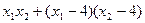
 ………9分
………9分
由方程(*)及韦达定理代入上式得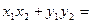
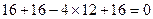 ………11分
………11分
所以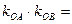
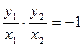 ,即
,即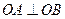
 ……………………12分
……………………12分
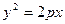
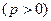 ,其准线方程为
,其准线方程为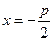 ,…2分
,…2分∵
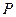 (4,
(4,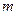 )到焦点的距离等于A到其准线的距离,
)到焦点的距离等于A到其准线的距离,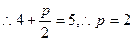
∴抛物线C的方程为
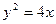 .
.  ………………………4分
………………………4分
(Ⅱ)由
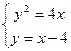 ,消去
,消去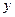 ,得
,得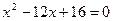 (*) ……………………6分
(*) ……………………6分∵直线
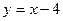 与抛物线相交于不同两点A、B,设
与抛物线相交于不同两点A、B,设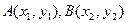 ,则有
,则有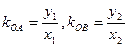
 ,则
,则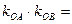
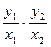 ………………………8分
………………………8分因为
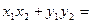
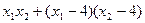
 ………9分
………9分由方程(*)及韦达定理代入上式得
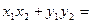
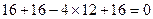 ………11分
………11分所以
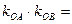
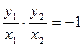 ,即
,即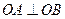
 ……………………12分
……………………12分略

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
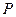 与点
与点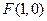 的距离和它到直线
的距离和它到直线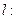
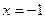 的距离相等,记点
的距离相等,记点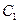 .圆
.圆
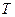 是曲线
是曲线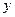 轴交于
轴交于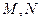 两点,且
两点,且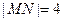 .
.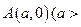 2
2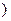 ,若点
,若点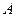 到点
到点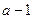 ,试判断直线
,试判断直线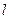 与圆
与圆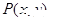 是曲线
是曲线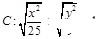 上的点,
上的点,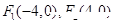 ,则
,则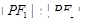 ( )
( )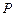 过点
过点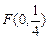 且与直线
且与直线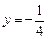 相切.
相切.
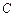 的方程;
的方程;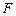 作一条直线交轨迹
作一条直线交轨迹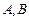 两点,轨迹
两点,轨迹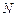 ,
,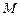 为线段
为线段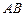 的中点,求证:
的中点,求证: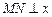 轴.
轴.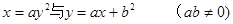 的图像只可能是下图中( *** )
的图像只可能是下图中( *** )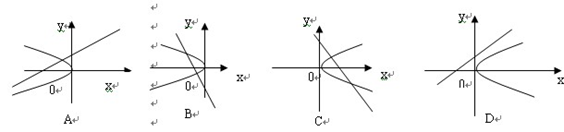
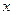 轴,
轴,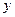 轴上的动点,P在直线AB上,且
轴上的动点,P在直线AB上,且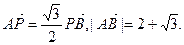
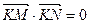 ,试证:直线MN必过
,试证:直线MN必过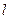 与中心在原点,焦点在x轴上且离心率为
与中心在原点,焦点在x轴上且离心率为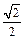 的椭圆C相
的椭圆C相 交于A、B两点,直线y=
交于A、B两点,直线y=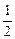 x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l
x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l 对称,试求直线l与椭圆C的方程
对称,试求直线l与椭圆C的方程
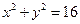 上任一点连线的中点轨迹方程是
上任一点连线的中点轨迹方程是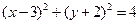
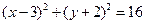
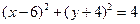
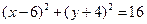
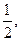 求点M的轨迹方程。
求点M的轨迹方程。