题目内容
(本小题满分12分)
已知定点A(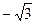 ,0),B是圆C:(x-
,0),B是圆C:(x-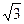 )2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
(1)求动点E的轨迹方程.
(2)设直线l:y="kx+m" (k≠0,m>0)与E的轨迹交与P,Q两点,且以PQ为对角线的菱形的一顶点为M(-1,0),求△OPQ面积的最大值及此时直线l的方程.
已知定点A(
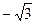 ,0),B是圆C:(x-
,0),B是圆C:(x-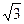 )2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.
)2+y2=16,(C为圆心)上的动点,AB的垂直平分线与BC交与点E.(1)求动点E的轨迹方程.
(2)设直线l:y="kx+m" (k≠0,m>0)与E的轨迹交与P,Q两点,且以PQ为对角线的菱形的一顶点为M(-1,0),求△OPQ面积的最大值及此时直线l的方程.
(1)
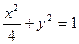
(2)
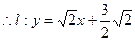
解:(1)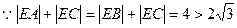
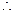 点E的轨迹是以B,C为焦点的椭圆
点E的轨迹是以B,C为焦点的椭圆
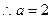

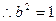
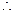 椭圆方程为
椭圆方程为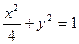 --------(4分)
--------(4分)
(2)设点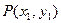
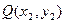 中点
中点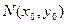

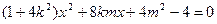
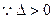
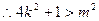
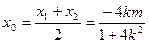
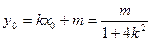
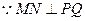
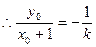
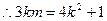
由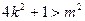 可得
可得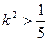
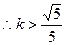
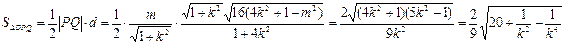
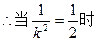
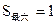 此时
此时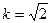 ,
,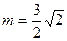
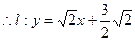 -------------------------------------------------(12分)
-------------------------------------------------(12分)
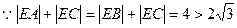
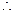 点E的轨迹是以B,C为焦点的椭圆
点E的轨迹是以B,C为焦点的椭圆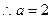

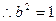
 椭圆方程为
椭圆方程为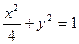 --------(4分)
--------(4分)(2)设点
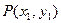
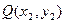 中点
中点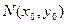

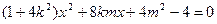
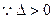
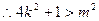
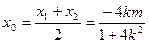
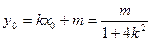
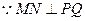
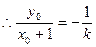
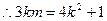
由
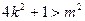 可得
可得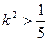
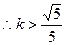
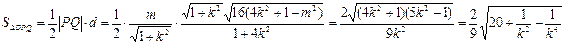
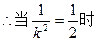
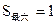 此时
此时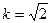 ,
,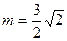
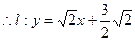 -------------------------------------------------(12分)
-------------------------------------------------(12分)
练习册系列答案
相关题目
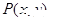 是曲线
是曲线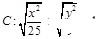 上的点,
上的点,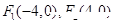 ,则
,则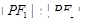 ( )
( )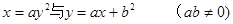 的图像只可能是下图中( *** )
的图像只可能是下图中( *** )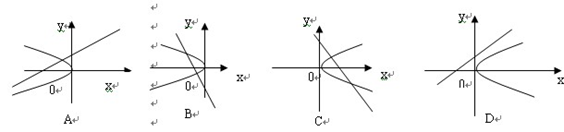
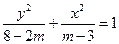 表示曲线C.
表示曲线C.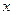 轴,
轴,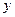 轴上的动点,P在直线AB上,且
轴上的动点,P在直线AB上,且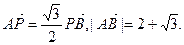
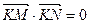 ,试证:直线MN必过
,试证:直线MN必过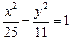 的左支上,
的左支上,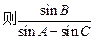 等于
等于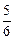
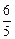
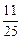
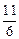
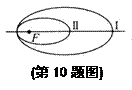
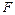 的椭圆Ⅰ与Ⅱ的长半轴的长分别为
的椭圆Ⅰ与Ⅱ的长半轴的长分别为 和
和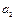 ,半焦距分别为
,半焦距分别为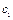 和
和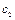 ,则下列结论不正确的是( )
,则下列结论不正确的是( )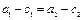
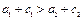
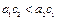
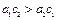
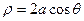 ,则各弦中点的轨迹方程为__________.
,则各弦中点的轨迹方程为__________.