题目内容
【题目】已知函数f（x）=x2+ 
，现有一组数据，绘制得到茎叶图，且茎叶图中的数据的平均数为2．（茎叶图中的数据均为小数，其中茎为整数部分，叶为小数部分） 
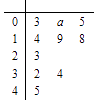
（Ⅰ）求a的值；
（Ⅱ）现从茎叶图小于3的数据中任取2个数据分别替换m的值，求恰有1个数据使得函数f（x）没有零点的概率．
【答案】解：（Ⅰ）根据茎叶图中的数据，计算平均数为 
= 
×（0.3+0.1×a+0.5+1.4+1.9+1.8+2.3+3.2+3.4+4.5）=2，
解得a=7；
（Ⅱ）茎叶图小于3的数据有0.3，0.7，0.5，1.4，1.9，1.8，2.3共7个；
从中任取2个数据，有 
=21种不同的取法；
函数f（x）=x2+ 
中，
△=2（m﹣1）2﹣m=2m2﹣5m+2，
令△＜0，解得 
＜m＜2，
∴满足该条件的数据是0.7，1.4，1.8，1.9共4个；
用抽出的2个数分别替换m的值，恰有1个数据使得函数f（x）没有零点的不同取法是 
=12，
故所求的概率为P= 
= 
．
【解析】（Ⅰ）根据茎叶图中的数据，利用平均数的定义列方程求出a的值；（Ⅱ）写出茎叶图小于3的数据，从中任取2个数据的不同取法； 利用判别式△＜0求出函数f（x）没有零点时m的取值范围，求出对应的事件数，
计算所求的概率值．
【考点精析】解答此题的关键在于理解茎叶图的相关知识，掌握茎叶图又称“枝叶图”，它的思路是将数组中的数按位数进行比较，将数的大小基本不变或变化不大的位作为一个主干（茎），将变化大的位的数作为分枝（叶），列在主干的后面，这样就可以清楚地看到每个主干后面的几个数，每个数具体是多少．
练习册系列答案
相关题目
