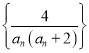Question

【题目】如图，在三棱锥P—ABC中，△PBC为等边三角形，点O为BC的中点，AC⊥PB，平面PBC⊥平面ABC．

（1）求直线PB和平面ABC所成的角的大小；

（2）求证：平面PAC⊥平面PBC；

（3）已知E为PO的中点，F是AB上的点，AF＝AB．若EF∥平面PAC，求的值．

Answer 1

【答案】（1）；（2）证明见解析；（3）

【解析】

（1）先找到直线PB与平面ABC所成的角为,再求其大小；（2）先证明,

再证明平面PAC⊥平面PBC；（3）取CO的中点G,连接EG,过点G作FG||AC,再求出的值.

（1）因为平面PBC⊥平面ABC，PO⊥BC, 平面PBC∩平面ABC=BC,,

所以PO⊥平面ABC,

所以直线PB与平面ABC所成的角为,

因为，

所以直线PB与平面ABC所成的角为.

(2)因为PO⊥平面ABC,

所以,

因为AC⊥PB，,

所以AC⊥平面PBC,

因为平面PAC,

所以平面PAC⊥平面PBC.

(3)

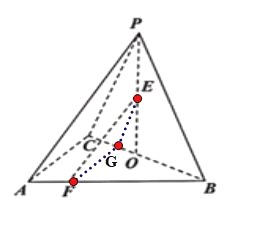
取CO的中点G,连接EG,过点G作FG||AC,

由题得EG||PC,所以EG||平面APC,

因为FG||AC，所以FG||平面PAC,

EG,FG平面EFO,EG∩FG=G,

所以平面EFO||平面PAC,

因为EF平面EFO,

所以EF||平面PAC.

此时AF=.