题目内容
【题目】在△ABC中，AB⊥BC，BA＝BC
，BD是边AC上的高，沿BD将△ABC折起，当三棱锥A﹣BCD的体积最大时，该三棱锥外接球表面积为（ ）
A. 12πB. 24πC. 36πD. 48π
【答案】A
【解析】
要使三棱锥A﹣BCD体积最大，则AD⊥平面BDC，利用补形法将三棱锥补成分别以
边的正方体，正方体的外接球就是该三棱锥的外接球，求得正方体的外接球半径为
，问题得解。
解：如图，
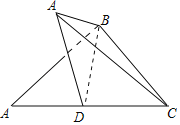
在Rt△ABC中，由AB⊥BC，BA＝BC
，得AC＝4，
∴AD＝DC＝BD＝2．
要使三棱锥A﹣BCD体积最大，则AD⊥平面BDC，
利用补形法将三棱锥补成分别以边的正方体，正方体的外接球就是该三棱锥的外接球
可得三棱锥A﹣BCD的外接球的半径R
．
∴该三棱锥的外接球的表面积为
．
故选：A．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
