题目内容
【题目】已知圆C:x2+y2+kx+2y+k2=0,过点P(1,﹣1)可作圆的两条切线,则实数k的取值范围是_____.
【答案】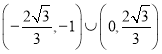
【解析】
利用方程x2+y2+kx+2y+k2=0表示一个圆可得:![]() ,解得:
,解得:![]() ,再利过点P(1,﹣1)可作圆的两条切线可得:P(1,﹣1)在圆的外部,可得:12+(﹣1)2+k﹣2+k2>0,解得:k<﹣1或k>0,问题得解。
,再利过点P(1,﹣1)可作圆的两条切线可得:P(1,﹣1)在圆的外部,可得:12+(﹣1)2+k﹣2+k2>0,解得:k<﹣1或k>0,问题得解。
解:因为方程x2+y2+kx+2y+k2=0表示一个圆,
所以![]() ,解得:
,解得:![]()
∵过点P(1,﹣1)可作圆C:x2+y2+kx+2y+k2=0的两条切线,
∴P(1,﹣1)在圆的外部,
则12+(﹣1)2+k﹣2+k2>0,
即k2+k>0,解得k<﹣1或k>0.
由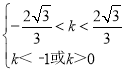 可得:
可得:![]() 或
或![]()
∴实数k的取值范围是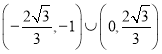
故答案为: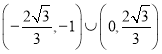

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目