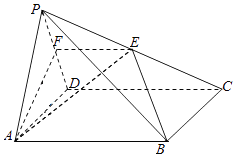
题目内容
【题目】椭圆![]() 一个焦点为
一个焦点为![]() ,离心率
,离心率![]() .
.
(Ⅰ)求椭圆![]() 的方程式.
的方程式.
(Ⅱ)定点![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,求
上的动点,求![]() 的最大值;并求出取最大值时
的最大值;并求出取最大值时![]() 点的坐标求.
点的坐标求.
(Ⅲ)定直线![]() ,
,![]() 为椭圆
为椭圆![]() 上的动点,证明点
上的动点,证明点![]() 到
到![]() 的距离与到定直线
的距离与到定直线![]() 的距离的比值为常数,并求出此常数值.
的距离的比值为常数,并求出此常数值.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ;(2)
;(2)![]() 最大值为
最大值为![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;(3)
;(3)![]() 到
到![]() 的距离与到定直线的距离之比为常数
的距离与到定直线的距离之比为常数![]() .
.
【解析】分析:(Ⅰ)由椭圆![]() 一个焦点为
一个焦点为![]() ,可知椭圆的焦点在
,可知椭圆的焦点在![]() 轴上,且
轴上,且![]() 。进而由离心率
。进而由离心率![]() ,可得
,可得![]() 。再由
。再由![]() 求得
求得![]() 。可得椭圆
。可得椭圆![]() 的方程为
的方程为![]() 。(Ⅱ)要求
。(Ⅱ)要求![]() 的最大值,应设坐标,用两点间的距离公式表示出来,然后求最值。
的最大值,应设坐标,用两点间的距离公式表示出来,然后求最值。
设![]() 点坐标为
点坐标为![]() ,则
,则![]() 。进而可得
。进而可得![]() ,由椭圆的性质可得
,由椭圆的性质可得![]() ,由二次函数的性质可得当
,由二次函数的性质可得当![]() 时,
时,![]() 取得最大值
取得最大值![]() .此时
.此时![]() 点坐标为
点坐标为![]() 。
。
(Ⅲ)设![]() 点
点![]() ,则
,则![]() ,所以
,所以![]() 点到
点到![]() 的距离为:
的距离为:![]() ,由椭圆的性质可得
,由椭圆的性质可得![]() 的范围,所以
的范围,所以 ![]() 。可得点
。可得点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,进而可得
,进而可得![]() ,所以
,所以![]() 到
到![]() 的距离与到定直线的距离之比为常数
的距离与到定直线的距离之比为常数![]() 。
。
详解:(Ⅰ)根据题意得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]()
故椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() 点坐标为
点坐标为![]() ,则
,则![]() ,
,
所以![]()
所以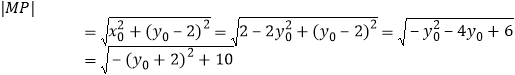 ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
∴![]() 最大值为
最大值为![]() ,此时
,此时![]() 点坐标为
点坐标为![]() .
.
(Ⅲ)设![]() 点
点![]() ,则
,则![]() ,
,
所以![]()
所以点![]() 到
到![]() 的距离为:
的距离为: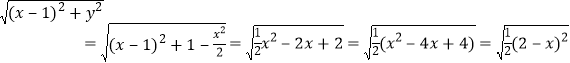 ,
,
由椭圆的性质可得![]()
所以![]()
所以点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
故![]() 到
到![]() 的距离与到定直线的距离之比为常数
的距离与到定直线的距离之比为常数![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目