题目内容
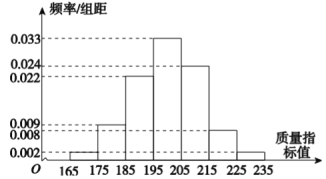
【题目】如图,长为![]() ,宽为
,宽为![]() 的矩形纸片
的矩形纸片![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转
翻转![]() (
(![]() 平面
平面![]() ),若
),若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,下列说法错误的是( )
翻转过程中,下列说法错误的是( )

A. ![]() 平面
平面![]()
B. 异面直线![]() 与
与![]() 所成角是定值
所成角是定值
C. 三棱锥![]() 体积的最大值是
体积的最大值是![]()
D. 一定存在某个位置,使![]()
【答案】D
【解析】
对于A,延长![]() ,
,![]() 交于
交于![]() ,连接
,连接![]() ,运用中位线定理和线面平行的判定定理,可得
,运用中位线定理和线面平行的判定定理,可得![]() 平面
平面![]() ;对于B,运用平行线的性质和解三角形的余弦定理,以及异面直线所成角的定义,求出异面直线所成的角;对于C,由题意知平面
;对于B,运用平行线的性质和解三角形的余弦定理,以及异面直线所成角的定义,求出异面直线所成的角;对于C,由题意知平面![]() 平面
平面![]() 时,三棱锥
时,三棱锥![]() 的体积最大,求出即可;对于D,连接
的体积最大,求出即可;对于D,连接![]() ,运用线面垂直的判定定理和性质定理,可得
,运用线面垂直的判定定理和性质定理,可得![]() 与
与![]() 垂直,可得结论;
垂直,可得结论;
由题意,对于![]() ,延长
,延长![]() ,
,![]() 交于
交于![]() ,连接
,连接![]() ,由
,由![]() 为
为![]() 的中点,
的中点,
可得![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 的中点,可得
的中点,可得![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,∴
,∴![]() 正确;
正确;
对于![]() ,
,![]() ,过
,过![]() 作
作![]() ,
,![]() 平面
平面![]() ,
,
则![]() 是异面直线
是异面直线![]() 与
与![]() 所成的角或所成角的补角,且
所成的角或所成角的补角,且![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
则![]() ,
,
则![]() 为定值,即
为定值,即![]() 为定值,∴
为定值,∴![]() 正确;
正确;
对于![]() ,设
,设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,由直角三角形斜边的中线长为斜边的一半,可得
,由直角三角形斜边的中线长为斜边的一半,可得
平面![]() ⊥平面
⊥平面![]() 时,三棱锥
时,三棱锥![]() 的体积最大,
的体积最大,
最大体积为![]() ,∴
,∴![]() 正确;
正确;
对于![]() ,连接
,连接![]() ,可得
,可得![]() ,若
,若![]() ,即有
,即有![]() 平面
平面![]() ,
,
即有![]() ,由
,由![]() 在平面
在平面![]() 中的射影为
中的射影为![]() ,
,
可得![]() 与
与![]() 垂直,但
垂直,但![]() 与
与![]() 不垂直,则不存在某个位置,使
不垂直,则不存在某个位置,使![]() ,∴
,∴![]() 错误;
错误;
故选:D.

【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?