题目内容
【题目】已知函数
（Ⅰ）若函数
的图像在点
处的切线与直线
平行，求实数
的值；
（Ⅱ）讨论函数
的单调性；
（Ⅲ）若在函数
定义域内，总有
成立，试求实数
的最大值.
【答案】(Ⅰ) 
；(Ⅱ)证明见解析；(Ⅲ) 
【解析】试题分析：（1）先根据导数几何意义得
，解得实数
的值；（2）求导数并分解因式，根据a与1的大小分类讨论导函数符号，根据导函数符号确定函数
的单调性；（3）先化简不等式，并根据不等式恒成立转化为对应函数最值问题： 
最大值不大于零，再利用导数求得函数最值
从而有
的最大值，最后利用导数求得
最大值，即得实数
的最大值.
试题解析：（Ⅰ）易得
，且
由题意，得
，解得
，
（Ⅱ）由（Ⅰ）得
，
①当
时， 
， 
函数
在
单调递减，
②当
时，由
，得
；
由
，得
或
函数
在
上单调递增，在
上单调递减.
③当
时，同理，得
函数
在
上单调递增，在
上单调递减，
综上，当
时，函数
在
单调递减；
当
时，函数
在
上单调递增，在
上单调递减；
当
时，函数
在
上单调递增，在
上单调递减.
（Ⅲ）由题意，知
恒成立，
恒成立，
恒成立，
令
，则只需
，
由
，得
，
当
时， 
，此时，函数
在
上单调递减；
当
时， 
，此时，函数
在
上单调递减，
令
，则只需
由
，得
，此时， 
在
上单调递减，
由
，得
，此时， 
在
上单调递减，
，
即
故所求实数
的最大值为
【题目】某特色餐馆开通了美团外卖服务，在一周内的某特色菜外卖份数
（份）与收入
（元）之间有如下的对应数据：
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计外卖份数为12份时，收入为多少元．
注：①参考公式：线性回归方程系数公式
， 
；
②参考数据： 
， 
， 
．
【题目】某特色餐馆开通了美团外卖服务，在一周内的某特色菜外卖份数
（份）与收入
（元）之间有如下的对应数据：
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）求回归直线方程；
（3）据此估计外卖份数为12份时，收入为多少元．
注：①参考公式：线性回归方程系数公式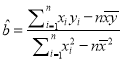
， 
；
②参考数据： 
， 
， 
．