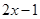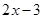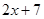题目内容
设a∈R,函数f(x)=lnx-ax.
(1)讨论函数f(x)的单调区间和极值;
(2)已知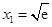 (e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e
(e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e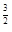 .
.
(1)讨论函数f(x)的单调区间和极值;
(2)已知
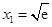 (e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e
(e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e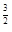 .
.解:(1)当a≤0时,f(x)的递增区间为(0,+∞),无极值;当a>0时,f(x)的递增区间为(0,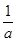 ),递减区间为(
),递减区间为(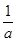 ,+∞),极大值为-lna-1.…(6分)
,+∞),极大值为-lna-1.…(6分)
(2)a=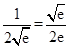 .
.
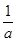 ),递减区间为(
),递减区间为(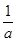 ,+∞),极大值为-lna-1.…(6分)
,+∞),极大值为-lna-1.…(6分)(2)a=
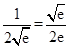 .
.掌握导数与函数单调性的关系,会熟练运用导数解决函数的极值与最值问题.
(1)首先求出函数的导数,然后根据导数与单调区间的关系确定函数的单调区间;得到极值;(2)由上知函数f(x)在(2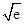 ,+∞)上单调递减,从而可证.
,+∞)上单调递减,从而可证.
(1)首先求出函数的导数,然后根据导数与单调区间的关系确定函数的单调区间;得到极值;(2)由上知函数f(x)在(2
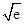 ,+∞)上单调递减,从而可证.
,+∞)上单调递减,从而可证.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 .
.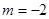 时,求
时,求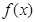 的单调区间;
的单调区间;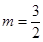 时,不等式
时,不等式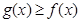 恒成立,求实数
恒成立,求实数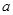 的取值范围.
的取值范围.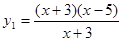 ,
,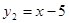 ; (2)
; (2) 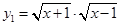 ,
,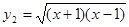
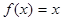 ,
,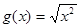 ; (4)
; (4)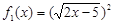 ,
,

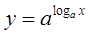
 ,且
,且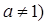
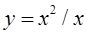
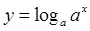
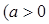 ,且
,且
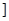 上是减函数,则实数a的取值范围是( )
上是减函数,则实数a的取值范围是( ) -
- ,+∞) B (-∞,-
,+∞) B (-∞,- 上的函数
上的函数 是奇函数(
是奇函数( ),则
),则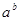 的取值范围是
的取值范围是 


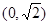
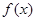 是
是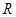 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当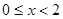 时,
时, ,则函数
,则函数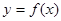 的图象在区间
的图象在区间 上与
上与 轴的交点的个数为 .
轴的交点的个数为 .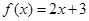 ,
,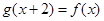 ,则函数
,则函数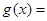 ( )
( )