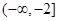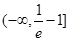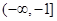题目内容
(本小题满分12分)
已知函数
 .
.
(1)当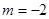 时,求
时,求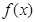 的单调区间;
的单调区间;
(2)若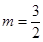 时,不等式
时,不等式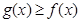 恒成立,求实数
恒成立,求实数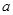 的取值范围.
的取值范围.
已知函数

 .
.(1)当
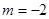 时,求
时,求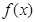 的单调区间;
的单调区间;(2)若
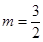 时,不等式
时,不等式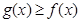 恒成立,求实数
恒成立,求实数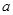 的取值范围.
的取值范围.(1)f(x)的单调递增区间是(e,+∞),递减区间是(0,e).(2)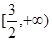 .
.
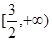 .
. (1)当m=-2时,解析式确定,可以求导,利用导数大(小)于零,求出单调增(减)区间,同时要注意函数的定义域.
(2)当m=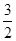 时,不等式g(x)≥f(x),即
时,不等式g(x)≥f(x),即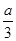 x3+x≥x
x3+x≥x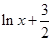 恒成立.
恒成立.
由于x>0,所以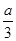 x2+1≥ln x+
x2+1≥ln x+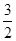 ,亦即
,亦即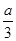 x2≥ln x+
x2≥ln x+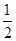 ,所以a≥
,所以a≥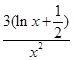 ,
,
然后构造函数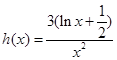 ,转化为利用导数研究其单调性,极值,最大值即可.
,转化为利用导数研究其单调性,极值,最大值即可.
(1)当m=-2时,f(x)=x(ln x-2)=xln x-2x,
定义域为(0,+∞),且f′(x)=ln x-1.
由f′(x)>0,得ln x-1>0,所以x>e.由f′(x)<0,得ln x-1<0,所以0<x<e.
故f(x)的单调递增区间是(e,+∞),递减区间是(0,e).
(2)当m=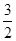 时,不等式g(x)≥f(x),即
时,不等式g(x)≥f(x),即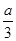 x3+x≥x
x3+x≥x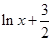 恒成立.
恒成立.
由于x>0,所以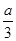 x2+1≥ln x+
x2+1≥ln x+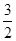 ,亦即
,亦即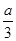 x2≥ln x+
x2≥ln x+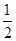 ,所以a≥
,所以a≥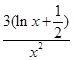 .
.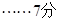
令h(x)=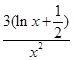 ,则h′(x)=
,则h′(x)=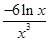 ,由h′(x)=0得x=1.
,由h′(x)=0得x=1.
且当0<x<1时,h′(x)>0;当x>1时,h′(x)<0,
即h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以h(x)在x=1处取得极大值h(1)=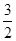 ,也就是函数h(x)在定义域上的最大值.因此要使
,也就是函数h(x)在定义域上的最大值.因此要使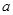 ≥
≥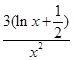 恒成立,需有
恒成立,需有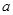 ≥
≥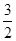 ,
,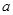 的取值范围为
的取值范围为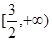 .
.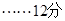
(2)当m=
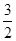 时,不等式g(x)≥f(x),即
时,不等式g(x)≥f(x),即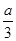 x3+x≥x
x3+x≥x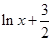 恒成立.
恒成立.由于x>0,所以
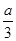 x2+1≥ln x+
x2+1≥ln x+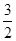 ,亦即
,亦即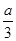 x2≥ln x+
x2≥ln x+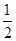 ,所以a≥
,所以a≥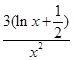 ,
,然后构造函数
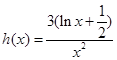 ,转化为利用导数研究其单调性,极值,最大值即可.
,转化为利用导数研究其单调性,极值,最大值即可.(1)当m=-2时,f(x)=x(ln x-2)=xln x-2x,
定义域为(0,+∞),且f′(x)=ln x-1.
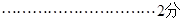
由f′(x)>0,得ln x-1>0,所以x>e.由f′(x)<0,得ln x-1<0,所以0<x<e.
故f(x)的单调递增区间是(e,+∞),递减区间是(0,e).
(2)当m=
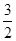 时,不等式g(x)≥f(x),即
时,不等式g(x)≥f(x),即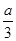 x3+x≥x
x3+x≥x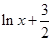 恒成立.
恒成立.由于x>0,所以
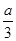 x2+1≥ln x+
x2+1≥ln x+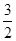 ,亦即
,亦即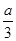 x2≥ln x+
x2≥ln x+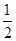 ,所以a≥
,所以a≥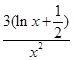 .
.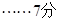
令h(x)=
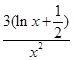 ,则h′(x)=
,则h′(x)=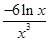 ,由h′(x)=0得x=1.
,由h′(x)=0得x=1.且当0<x<1时,h′(x)>0;当x>1时,h′(x)<0,
即h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以h(x)在x=1处取得极大值h(1)=
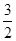 ,也就是函数h(x)在定义域上的最大值.因此要使
,也就是函数h(x)在定义域上的最大值.因此要使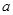 ≥
≥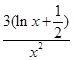 恒成立,需有
恒成立,需有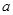 ≥
≥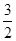 ,
,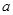 的取值范围为
的取值范围为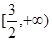 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
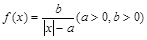 的图象形如汉字“囧”,故称其为“囧函数”.下列命题正确的是 .
的图象形如汉字“囧”,故称其为“囧函数”.下列命题正确的是 .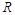 ; ②“囧函数”在
; ②“囧函数”在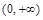 上单调递增;
上单调递增;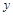 轴对称; ④“囧函数”有两个零点;
轴对称; ④“囧函数”有两个零点;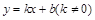 的图象至少有一个交点.
的图象至少有一个交点.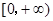 是定义在上的减函数,且
是定义在上的减函数,且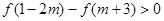 ,求实数
,求实数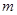 的取值范围。
的取值范围。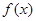 是定义在R上的奇函数,且当x
是定义在R上的奇函数,且当x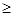 0时,
0时,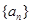 是等差数列,且a3<0,则
是等差数列,且a3<0,则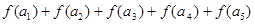 的值为:
的值为: 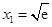 (e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e
(e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e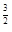 .
.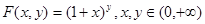 .
.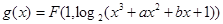 的图象为曲线
的图象为曲线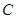 ,若存在实数
,若存在实数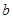 ,使得曲线
,使得曲线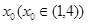 处有斜率是
处有斜率是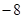 的切线,求实数
的切线,求实数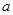 的取值范围;
的取值范围;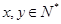 ,且
,且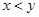 时,证明:
时,证明: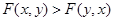 .
.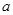 是函数f(x)=
是函数f(x)=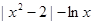 在定义域内的最小零点,若
在定义域内的最小零点,若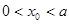 ,则
,则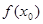 的值满足 ( )
的值满足 ( )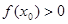
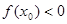
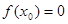
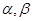 是关于
是关于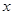 的方程
的方程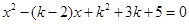 的两根,求
的两根,求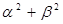 的最大值和最小值.
的最大值和最小值.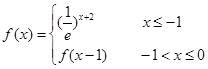 , 若f (x)≥x+a“对于任意x∈R恒成立,则常数a的取值范围是( )
, 若f (x)≥x+a“对于任意x∈R恒成立,则常数a的取值范围是( )