题目内容
已知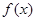 是
是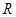 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当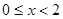 时,
时, ,则函数
,则函数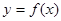 的图象在区间
的图象在区间 上与
上与 轴的交点的个数为 .
轴的交点的个数为 .
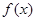 是
是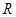 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当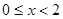 时,
时, ,则函数
,则函数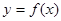 的图象在区间
的图象在区间 上与
上与 轴的交点的个数为 .
轴的交点的个数为 .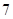
因为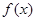 是
是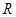 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当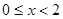 时,
时, ,则函数
,则函数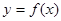 的图象在区间
的图象在区间 上与
上与 轴的交点的个数为7,故答案为7
轴的交点的个数为7,故答案为7
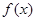 是
是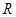 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当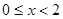 时,
时, ,则函数
,则函数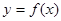 的图象在区间
的图象在区间 上与
上与 轴的交点的个数为7,故答案为7
轴的交点的个数为7,故答案为7
练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
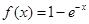
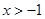 时,
时,
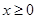 时,
时, ,求
,求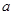 的取值范围。
的取值范围。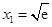 (e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e
(e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e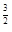 .
.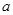 是函数f(x)=
是函数f(x)=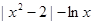 在定义域内的最小零点,若
在定义域内的最小零点,若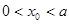 ,则
,则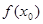 的值满足 ( )
的值满足 ( )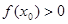
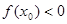
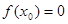
 上的函数
上的函数 满足:
满足: ,当
,当 时,
时, .下列四个不等关系中正确的是( )
.下列四个不等关系中正确的是( )



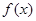 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件: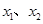 、
、 是定义域中的数时,有
是定义域中的数时,有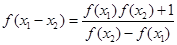 ;
;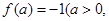
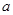 是定义域中的一个数);
是定义域中的一个数);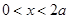 时,
时,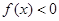 .
.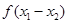 与
与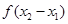 之间的关系,并推断函数
之间的关系,并推断函数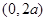 上的单调性,并证明;
上的单调性,并证明;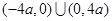 时,
时,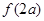 的值;②求不等式
的值;②求不等式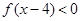 的解集.
的解集.  的定义域是
的定义域是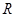 ,则实数
,则实数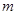 的取值范围是
的取值范围是 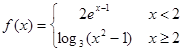 ,则不等式
,则不等式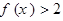 的解集为____________
的解集为____________