题目内容
3.在一批棉花中抽测了60根棉花的纤维长度,结果如下(单位:mm)| 82 | 202 | 352 | 321 | 25 | 293 | 293 | 86 | 28 | 206 |
| 323 | 355 | 357 | 33 | 325 | 113 | 233 | 294 | 50 | 296 |
| 115 | 236 | 357 | 326 | 52 | 301 | 140 | 328 | 238 | 358 |
| 58 | 255 | 143 | 360 | 340 | 302 | 370 | 343 | 260 | 303 |
| 59 | 146 | 60 | 263 | 170 | 305 | 380 | 346 | 61 | 305 |
| 175 | 348 | 264 | 383 | 62 | 306 | 195 | 350 | 265 | 385 |
分析 按照画频率分布直方图的基本步骤:(1)求极差,(2)确定组距与组数,(3)列频率分布表,(4)画频率分布直方图,画出图形;
根据频率分布直方图,得出频率估计与分析.
解答 解:(1)求极差,385-25=360;
(2)确定组距与组数,$\frac{360}{6}$=60,
分6组,组距为60;
(3)列频率分布表,如下表;
| 分组 | 频数 | 频率 |
| [25,85) | 11 | $\frac{11}{60}$ |
| [85,145) | 5 | $\frac{1}{12}$ |
| [145,205) | 5 | $\frac{1}{12}$ |
| [205,265) | 8 | $\frac{2}{15}$ |
| [265,325) | 13 | $\frac{13}{60}$ |
| [325,385] | 18 | $\frac{3}{10}$ |
| 总计 | 60 | 1.00 |
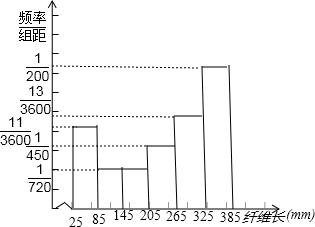
根据频率分布直方图,得;
该种棉花的纤维长度分布在25~385mm之间,其中纤维长度在265~385mm的棉花占一半多($\frac{31}{60}$).
点评 本题考查了画频率分布直方图的问题,也考查了利用频率分布直方图进行概率分析与估计的应用问题,是基础题目.

练习册系列答案
相关题目
17.设数列{an}的前n项和Sn=$\frac{n(n+1)}{2}$,则a5=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.给出以下两个类比推理(其中Q为有理数集,R为实数集,C为复数集)
①“若a,b∈R,则a-b>0⇒a>b”类比推出“a,b∈C,则a-b>0⇒a>b”
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b$\sqrt{2}=c+d\sqrt{2}$?a=c,b=d”;
对于以上类比推理得到的结论判断正确的是( )
①“若a,b∈R,则a-b>0⇒a>b”类比推出“a,b∈C,则a-b>0⇒a>b”
②“若a,b,c,d∈R,则复数a+bi=c+di⇒a=c,b=d”类比推出“若a,b,c,d∈Q,则a+b$\sqrt{2}=c+d\sqrt{2}$?a=c,b=d”;
对于以上类比推理得到的结论判断正确的是( )
| A. | 推理①②全错 | B. | 推理①对,推理②错 | C. | 推理①错,推理②对 | D. | 推理①②全对 |