题目内容
12.已知集合{(x,y)|x∈[0,3],y∈[-1,1]}(1)若x,y∈z,则3x+2y-1≥0概率为多少?
(2)若x,y∈R,则3x+2y-1≥0概率为多少?
分析 (1)由题意,x,y∈z,则x=0,1,2,3,y=-1,0,1,利用古典概型的概率公式解答;
(2)由x,y∈R,则是几何概型的概率求法,只要求出区域的面积以及满足条件的区域面积,利用面积比求概率.
解答 解:已知集合{(x,y)|x∈[0,3],y∈[-1,1]}
(1)x,y∈z,则x=0,1,2,3,y=-1,0,1,从中任意取一个组成点(x,y),共有4×3=12个,而满足3x+2y-1≥0点共有10个,则由古典概型的公式得到$\frac{10}{12}=\frac{5}{6}$;
(2)x,y∈R,则满足题意的区域面积为6,而满足3x+2y-1≥0区域如图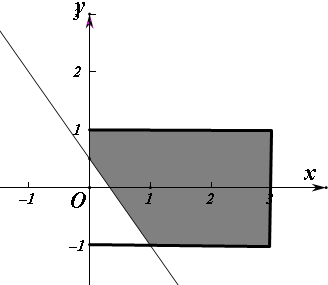 面积为6-$\frac{1}{2}×\frac{3}{2}×1$,概率为1-$\frac{\frac{3}{4}}{6}$=$\frac{7}{8}$.
面积为6-$\frac{1}{2}×\frac{3}{2}×1$,概率为1-$\frac{\frac{3}{4}}{6}$=$\frac{7}{8}$.
点评 本题主要考查几何概型中的面积类型和古典概型,两者最明显的区别是古典概型的基本事件是有限的,几何概型的基本事件是无限的.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
3.在一批棉花中抽测了60根棉花的纤维长度,结果如下(单位:mm)
作出这个样本的频率分布直方图(在对样本数据分组时,可试用不同的分组方式,然后从中选择一种较为适合的分组方法).棉花的纤维长度是棉花质量的重要指标,你能从图中分析出这批棉花的质量状况吗?
| 82 | 202 | 352 | 321 | 25 | 293 | 293 | 86 | 28 | 206 |
| 323 | 355 | 357 | 33 | 325 | 113 | 233 | 294 | 50 | 296 |
| 115 | 236 | 357 | 326 | 52 | 301 | 140 | 328 | 238 | 358 |
| 58 | 255 | 143 | 360 | 340 | 302 | 370 | 343 | 260 | 303 |
| 59 | 146 | 60 | 263 | 170 | 305 | 380 | 346 | 61 | 305 |
| 175 | 348 | 264 | 383 | 62 | 306 | 195 | 350 | 265 | 385 |
20.若存在实数a,对任意实数x∈[0.m],均有(sinx-a)(cosx-a)≤0,则实数m的最大值是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{4}$ |
1.极坐标系中,圆ρ=2cosθ与直线2ρcos(θ+$\frac{π}{3}$)=-1的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
2.若一组数据a1,a2,…,an的方差是5,则一组新数据2a1,2a2,…,2an的方差是( )
| A. | 5 | B. | 10 | C. | 20 | D. | 50 |
 如图,直三棱柱ABC-A1B1C1侧棱长为2,底面边AC、BC的长均为2,且AC⊥BC,若D为BB1的中点,E为AC的中点,M为AB的中点,N为BC的中点.
如图,直三棱柱ABC-A1B1C1侧棱长为2,底面边AC、BC的长均为2,且AC⊥BC,若D为BB1的中点,E为AC的中点,M为AB的中点,N为BC的中点.