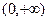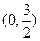题目内容
设函数fn(x)=n2x2(1－x)n(n为正整数)，则fn(x)在［0,1］上的最大值为( )
| A．0 | B．1 | C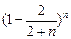． | D． |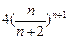
D
∵f′n(x)=2xn2(1－x)n－n3x2(1－x)n-1
=n2x(1－x)n-1［2(1－x)－nx］,
令f′n(x)=0,得x1=0,x2=1,x3=
,
易知fn(x)在x=时取得最大值，
最大值fn()=n2()2(1－)n=4·(
)n+1
=n2x(1－x)n-1［2(1－x)－nx］,
令f′n(x)=0,得x1=0,x2=1,x3=
,易知fn(x)在x=
时取得最大值，最大值fn(
)=n2()2(1－)n=4·()n+1
练习册系列答案
步步高达标卷系列答案
相关题目
.
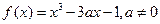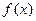的单调区间； 
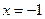处取得极值，直线
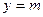与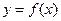
的图象有三个不同的交点，求
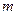的取值范围。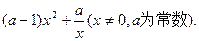
= 
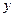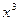－12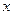
+16在 [－3,3]上的最大值、最小值分别是（ ）
，当
时取得极大值
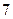，当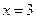
时取得极小值，求极小值及其对应的
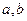的值。
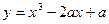在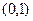
内有极小值，则实数
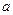的取值范围为（ ）
