题目内容
已知函数f(x)=x2e-ax(a>0),求函数在[1,2]上的最大值.
当0<a<1时,f(x)的最大值为4e-2a,当1≤a≤2时,f(x)的最大值为4a-2e-2,
当a>2时,f(x)的最大值为e-a.
当a>2时,f(x)的最大值为e-a.
∵f(x)=x2e-ax(a>0),
∴f′(x)=2xe-ax+x2·(-a)e-ax=e-ax(-ax2+2x). 3分
令f′(x)>0,即e-ax(-ax2+2x)>0,得0<x<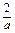 .
.
∴f(x)在(-∞,0),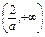 上是减函数,
上是减函数,
在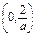 上是增函数.
上是增函数.
①当0<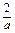 <1,即a>2时,f(x)在(1,2)上是减函数,
<1,即a>2时,f(x)在(1,2)上是减函数,
∴f(x)max=f(1)=e-a. 8分
②当1≤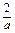 ≤2,即1≤a≤2时,
≤2,即1≤a≤2时,
f(x)在(1,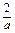 )上是增函数,在(
)上是增函数,在(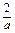 ,2)上是减函数,
,2)上是减函数,
∴f(x)max=f(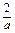 )=4a-2e-2. 12分
)=4a-2e-2. 12分
③当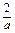 >2时,即0<a<1时,f(x)在(1,2)上是增函数,
>2时,即0<a<1时,f(x)在(1,2)上是增函数,
∴f(x)max=f(2)=4e-2a.
综上所述,当0<a<1时,f(x)的最大值为4e-2a,
当1≤a≤2时,f(x)的最大值为4a-2e-2,
当a>2时,f(x)的最大值为e-a. 14分
∴f′(x)=2xe-ax+x2·(-a)e-ax=e-ax(-ax2+2x). 3分
令f′(x)>0,即e-ax(-ax2+2x)>0,得0<x<
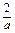 .
.∴f(x)在(-∞,0),
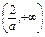 上是减函数,
上是减函数,在
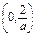 上是增函数.
上是增函数.①当0<
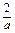 <1,即a>2时,f(x)在(1,2)上是减函数,
<1,即a>2时,f(x)在(1,2)上是减函数,∴f(x)max=f(1)=e-a. 8分
②当1≤
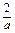 ≤2,即1≤a≤2时,
≤2,即1≤a≤2时,f(x)在(1,
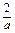 )上是增函数,在(
)上是增函数,在(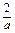 ,2)上是减函数,
,2)上是减函数,∴f(x)max=f(
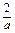 )=4a-2e-2. 12分
)=4a-2e-2. 12分③当
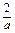 >2时,即0<a<1时,f(x)在(1,2)上是增函数,
>2时,即0<a<1时,f(x)在(1,2)上是增函数,∴f(x)max=f(2)=4e-2a.
综上所述,当0<a<1时,f(x)的最大值为4e-2a,
当1≤a≤2时,f(x)的最大值为4a-2e-2,
当a>2时,f(x)的最大值为e-a. 14分

练习册系列答案
相关题目
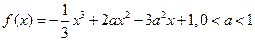 。
。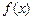 的极大值;
的极大值;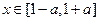 时,恒有
时,恒有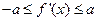 成立(其中
成立(其中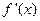 是函数
是函数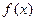 的导函数),试确定实数
的导函数),试确定实数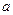 的取值范围。
的取值范围。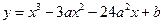 有正的极大值和负的极小值,其差为4,
有正的极大值和负的极小值,其差为4,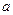 的值;
的值;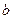 的取值范围.
的取值范围.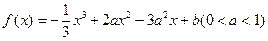
 ,求a的取值范围.
,求a的取值范围.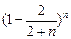
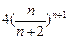
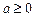 ,
,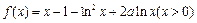 .令
.令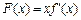 ,讨论
,讨论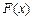 在
在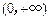 内的单调性并求极值;
内的单调性并求极值;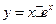 的最小值为 。
的最小值为 。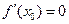 时,
时,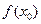 为
为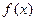 的极大值
的极大值